
����Ŀ�����ǰ���ƽ���ı��������ֱ�߳�Ϊ�����ߡ��������������ͼ�����Եõ��ı��εġ����ߡ�����ͼ1�ı���ABCD�У�ȡ�Խ���BD���е�O������OA��OC����Ȼ������AOC��ƽ���ı���ABCD��������ٹ���O��OE��AC��CD��E����ֱ��AE��Ϊһ�������ߡ���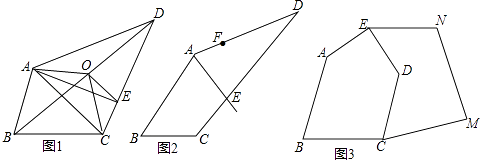
��1����ͼ1����˵��ֱ��AE�ǡ����ߡ������ɣ�
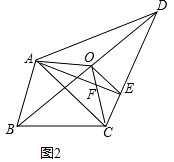
��2����ͼ2��AEΪһ�������ߡ���FΪAD���ϵ�һ�㣬����������F��ġ����ߡ�����˵�����ɣ�
��3����ͼ3�������ABCDE��һ�����ص�ʾ��ͼ���������꿪�ѻĵأ����ѱ����ͼ3��ʾ����״����ԭ�������뿪�ѻĵصķֽ�С·������CDE���������ţ����������E����һ��ֱ·��Ҫ��ֱ·��ߵ����������ԭ��һ���ֻࣨ�����ͼ�ʵ�˵������˵�����ɣ�
���𰸡�
��1���⣺�ߵ�O��BD���е㣬
��S��AOB=S��AOD��S��BOC=S��DOC��
��S��AOB+S��BOC=S��AOD+S��DOC= ![]() S�ı���ABCD��
S�ı���ABCD��
��S�ı���ABCO= ![]() S�ı���ABCD��
S�ı���ABCD��
������AOC��ƽ���ı���ABCD�������
��AE��OC��F��
��OE��AC��
��S��AOE=S��COE��
��S��AOF=S��CEF��
������AOC��ƽ���ı���ABCD�������
��ֱ��AEƽ���ı���ABCD���������AE���ı���ABCD��һ�������ߡ���
��2���⣺����EF����A��EF��ƽ���߽�CD�ڵ�G������FG����GFΪһ�������ߡ���

��AG��EF��
��S��AGE=S��AFG��
��AE��FG�Ľ�����O����S��AOF=S��GOE��
��AEΪһ�������ߡ�������GFΪһ�������ߡ���
��3���⣺��ͼ3��
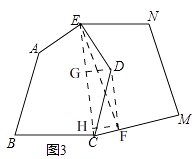
����CE������D��DF��EC��CM��F������EF����EFΪ����ֱ·��
���ɣ�����D��DG��CE��G������F��FH��EC��H��
��DF��EC����DG=FH������ƽ����ľ��봦����ȣ���
��S��CDE= ![]() EC��DG��S��CEF=
EC��DG��S��CEF= ![]() EC��FH��
EC��FH��
��S��CDE=S��CEF��
��S�ı���ABCDE=S�ı���ABCE+S��CDE=S�ı���ABCE+S��CEF=S�����ABCFE��
����ֱ·��ߵ����������ԭ��һ���࣮
����������1��������AH��BC������ΪH�����������ε������ʽ�ɵõ�S��ABD=![]() BDAH��S��ADC=
BDAH��S��ADC=![]() DCAH��Ȼ��������BD=CD���ɵõ�S��ABD=S��ADC�����жϳ�S�ı���ABCO=
DCAH��Ȼ��������BD=CD���ɵõ�S��ABD=S��ADC�����жϳ�S�ı���ABCO=![]() S�ı���ABCD�������жϳ�S��AOE=S��COE���Ƴ�S��AOF=S��CEF�������Ƴ�ֱ��AEƽ���ı���ABCD�������
S�ı���ABCD�������жϳ�S��AOE=S��COE���Ƴ�S��AOF=S��CEF�������Ƴ�ֱ��AEƽ���ı���ABCD�������
��2����������EF��FG��Ȼ�����A��EF��ƽ���߽�CD�ڵ�G����AG��EF���Ƴ�S��AGE=S��AFG����AE��FG�Ľ�����O����S��AOF=S��GOE����AEΪһ�������ߡ�������GFΪһ�������ߡ���
��3����������CE��EF��Ȼ�����D��DF��EC��CM��F��Ȼ�����ݼ���ƽ����ľ��봦����ȵó�DG=FH�����ǿɵõ�S��CDE=S��CEF.
�����㾫����������Ҫ������ƽ����֮��ľ�������֪ʶ�㣬��Ҫ��������ƽ���ߵľ��룺����ֱ��ƽ�У���һ��ֱ���ϵ�����һ������һ��ֱ�������ߣ����߶εij��ȣ���������ƽ���ߵľ��������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��n���ε�ͬһ������������ֱ����������������������㣬�����������ηָ��6�������Σ���n��ֵ�ǣ� ��
A.6
B.7
C.8
D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ҵ�ϴ������װ��һ��̧��ʽˮ��ͷ����ͼ1������ȫ������ˮ��·�߳������ߣ����ֶ˵�A����ˮ��B����ˮ��Cǡ����ͬһֱ���ϣ���A����ˮ��BD�ľ���Ϊ12cm��ϴ���輰ˮ��ͷ�����������ͼ2��ʾ�����ø�10.2cm��Բ����ˮ��ȥ��ˮ����ˮ�����������߾�����D�ͱ����ϵ�������E�����E��ϴ�����ڲ�ľ���EHΪ_________cm��

����16��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˶�����־��߰༶��������ijУ���꼶ѧ������ȫ��μӡ�������ɽ һ·��ǰ������50����ͽ�����������㲽�г���20���Ӻ�������������ʦ�����г���2�����ٶ�ԭ·�ϣ�����ھ����10ǧ�״��ϣ���ѧ�����е��ٶȺ�����ʦ�����г����ٶȷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��һ�η��̣��飩��һԪһ�β���ʽ��һ�κ��������֪ʶ�����������£�
һ�κ����뷽�̵Ĺ�ϵ��
��һ�κ����Ľ���ʽ����һ����Ԫһ�η��̣�
�ڵ�B�ĺ������Ƿ������Ľ⣻
�۵�C�����꣨x��y���е�x��y��ֵ�Ƿ��������Ľ�
һ�κ����벻��ʽ�Ĺ�ϵ��
�ٺ���y=kx+b�ĺ���ֵyС��0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ���Ľ⼯��
�ں���y=kx+b�ĺ���ֵy����0ʱ���Ա���x��ȡֵ��Χ���Dz���ʽ���Ľ⼯��
��1����������Ϸ����е�������������ѧ��ź�д����Ӧ��ʽ�ӣ�
����������������
��2�������C������Ϊ��2��5������ô����ʽkx+b��k1x+b1�Ľ⼯�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�յ�Ǯ�����۲���Ϣ���£�

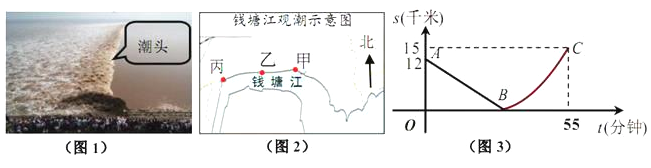
��������Ϣ��С�콫�����泱���γɺ�ͷ���ҵ��ʼ�ľ���![]() ��ǧ�ף���ʱ��
��ǧ�ף���ʱ��![]() �����ӣ��ĺ�����ϵ��ͼ3��ʾ.���У���11:40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��
�����ӣ��ĺ�����ϵ��ͼ3��ʾ.���У���11:40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��![]() ����
����![]() ����Ϊ
����Ϊ![]() ������
������![]() ���ö��κ�����s=
���ö��κ�����s=![]() ����
����![]() �dz������̻�.
�dz������̻�.
��1����![]() ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��2��11:59ʱ��С���ﵥ�����ҵس������ؽ��߹�·��![]() ǧ��/�ֵ��ٶ����ط���ȥ�����������������볱ͷ������
ǧ��/�ֵ��ٶ����ط���ȥ�����������������볱ͷ������
��3��������С��������ת��ͷ���ؽ��߹�·����ͷ�ٶ��볱ͷ���У�����ͷ���ҵغ���ȼ��٣�����������ٶ�Ϊ![]() ǧ��/�֣�С�������.��С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�
ǧ��/�֣�С�������.��С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�![]() ��
��![]() �Ǽ���ǰ���ٶȣ�.
�Ǽ���ǰ���ٶȣ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=2x��2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��1�����A��B�����ꣻ
��2����C��x���ϣ���S��ABC=3S��AOB �� ֱ��д����C���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ�����O��AB����O��ֱ������B=30����CEƽ����ACB����O��E����AB�ڵ�D������AE����S��ADE��S��CDB��ֵ���ڣ� ��
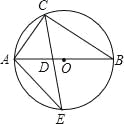
A. 1��![]() B. 1��
B. 1��![]() C. 1��2 D. 2��3
C. 1��2 D. 2��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com