
【题目】直线y=2x﹣2与x轴交于点A,与y轴交于点B.
(1)求点A、B的坐标;
(2)点C在x轴上,且S△ABC=3S△AOB , 直接写出点C坐标.
【答案】
(1)解:令y=2x﹣2中y=0,则2x﹣2=0,解得:x=1,
∴A(1,0).
令y=2x﹣2中x=0,则y=﹣2,
∴B(0,﹣2).
(2)解:依照题意画出图形,如图所示.
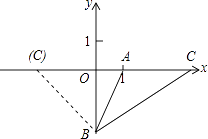
设点C的坐标为(m,0),
S△AOB= ![]() OAOB=
OAOB= ![]() ×1×2=1,S△ABC=
×1×2=1,S△ABC= ![]() ACOB=
ACOB= ![]() |m﹣1|×2=|m﹣1|,
|m﹣1|×2=|m﹣1|,
∵S△ABC=3S△AOB,
∴|m﹣1|=3,
解得:m=4或m=﹣2,
即点C的坐标为(4,0)或(﹣2,0).
【解析】(1)首先分别令y=2x-2中x=0、y=0,从而可求出与之对应的y、x值,故此可得出点A、B的坐标;
(2)首先设点C的坐标为(m,0),然后根据三角形的面积公式结合两三角形面积间的关系得出关于m含绝对值符号的一元一次方程,最后,解关于m的一元一次方程即可.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】下列式子正确的( )
A. x﹣(y﹣z)=x﹣y﹣zB. ﹣a+b+c+d=﹣(a﹣b)﹣(﹣c﹣d)
C. x+2y﹣2z=x﹣2(z+y)D. ﹣(x﹣y+z)=﹣x﹣y﹣z
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:如图1四边形ABCD中,取对角线BD的中点O,连接OA,OC,显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.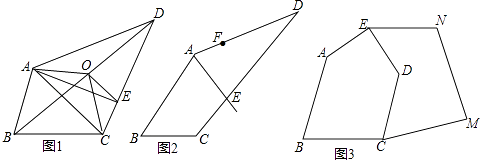
(1)如图1,试说明直线AE是“好线”的理由;
(2)如图2,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并说明理由;
(3)如图3,五边形ABCDE是一块土地的示意图,经过多年开垦荒地,现已变成如图3所示的形状,但原块土地与开垦荒地的分界小路(折线CDE)还保留着,现在请你过E点修一条直路.要求直路左边的土地面积与原来一样多(只需对作图适当说明无需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算75°23′12″﹣46°53′43″=( )
A. 28°70′69″B. 28°30′29″C. 29°30′29″D. 28°29′29″
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
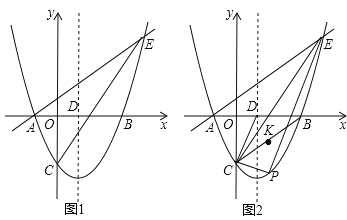
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲种物品每个重4 kg,乙种物品每个重7 kg,现有甲种物品x个,乙种物品y个,共重76 kg.
(1)列出关于x,y的二元一次方程;
(2)若x=12,则y=_______;
(3)若乙种物品有8个,则甲种物品有_______个;
(4)写出满足条件的x,y的全部整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.求小明和小张每分钟各打多少个字?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com