
����Ŀ��������ABCD�У���B=60�㣬AB=4������M��ÿ��1����λ���ٶȴӵ�A�����˶�����B����N����ͬ���ٶȴӵ�B�����˶�����C������ͬʱ����������M��MP��AB��ֱ��CD�ڵ�P������NM��NP�����˶�ʱ��Ϊt�룮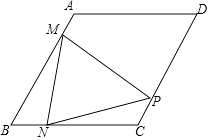
��1����t=2ʱ����NMP=�ȣ�
��2����tΪ��ֵʱ����A��M��C��PΪ������ı�����ƽ���ı��Σ�
��3������NPCΪֱ��������ʱ�����ʱt��ֵ��
���𰸡�
��1��30
��2���⣺����P���߶�CD��ʱ����A��AE��CD��E��
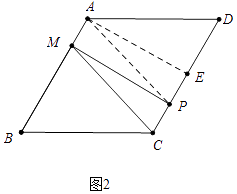
������ABCD�У�AB��CD����D=60�㣬AB=AD=CD=BC=4
��DE= ![]() AD=2��AE=2
AD=2��AE=2 ![]() ��
��
��AM=t��PC=2��t
Ҫʹ�ı���AMCPΪƽ���ı��Σ���AM=PC
��t=2��t��t=1��
����P���߶�DC�ӳ�����ʱ���ı���AMCP����ƽ���ı��Σ�
��3���⣺����P���߶�CD��ʱ��������Rt��NPC��
��ֻ�е�P���߶�DC�ӳ�����ʱ���Ŵ���Rt��NPC��
��ͼ3�У�����NPC=90��ʱ����M��N��P��ͬһֱ���ϣ�
���CNP=��MNB=30�㣬
��BM= ![]() BN����4��t=
BN����4��t= ![]() t��
t��
��ã�t= ![]() ��
��
��ͼ4�У�����PNC=90��ʱ��
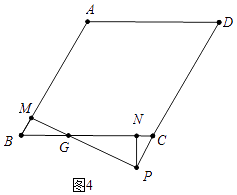
��֪BG=2��4��t����MG= ![]() ��4��t����
��4��t����
GN=t��2��4��t��=3t��8��GP=NG��cos30��= ![]() ��3t��8����
��3t��8����
��PM=2 ![]() ��
��
��MG+GP=2 ![]() ��
��
�� ![]() ��4��t��+
��4��t��+ ![]() ��3t��8��=2
��3t��8��=2 ![]() ��
��
���t=10���������⣬
����������t= ![]() sʱ����PNC��ֱ�������Σ�
sʱ����PNC��ֱ�������Σ�
���������⣺��1����ͼ1�У�����AC��
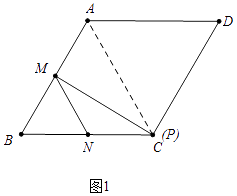
���ı���ABCD�����Σ���B=60�㣬
��AB=BC=CD=AD��
���ABC����ACD���ǵȱ������Σ�
��t=2ʱ��AM=BM=2��BN=CN=2��
��PM��AB��
��PA=PB��
��P��C�غϣ�
��MN��AC��
���NMP=��ACM= ![]() ��ACB=30�㣮
��ACB=30�㣮
��2������P���߶�CD��ʱ����A��AE��CD��E��

������ABCD�У�AB��CD����D=60�㣬AB=AD=CD=BC=4
��DE= ![]() AD=2��AE=2
AD=2��AE=2 ![]() ��
��
��AM=t��PC=2��t
Ҫʹ�ı���AMCPΪƽ���ı��Σ���AM=PC
��t=2��t��t=1��
����P���߶�DC�ӳ�����ʱ���ı���AMCP����ƽ���ı��Σ�
��3������P���߶�CD��ʱ��������Rt��NPC��
��ֻ�е�P���߶�DC�ӳ�����ʱ���Ŵ���Rt��NPC��
��ͼ3�У�����NPC=90��ʱ����M��N��P��ͬһֱ���ϣ�
���CNP=��MNB=30�㣬
��BM= ![]() BN����4��t=
BN����4��t= ![]() t��
t��
��ã�t= ![]() ��
��
��ͼ4�У�����PNC=90��ʱ��

��֪BG=2��4��t����MG= ![]() ��4��t����
��4��t����
GN=t��2��4��t��=3t��8��GP=NG��cos30��= ![]() ��3t��8����
��3t��8����
��PM=2 ![]() ��
��
��MG+GP=2 ![]() ��
��
�� ![]() ��4��t��+
��4��t��+ ![]() ��3t��8��=2
��3t��8��=2 ![]() ��
��
���t=10���������⣬
����������t= ![]() sʱ����PNC��ֱ�������Σ�
sʱ����PNC��ֱ�������Σ�
���Դ��ǣ���1��30����2��t=1����3��t=![]() .
.
�����㾫����ͨ���������ƽ���ı��ε����ʣ�����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ּ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+b������A����30��0���͵�B��0��15����ֱ��y=x+5��ֱ��y=kx+b�ཻ�ڵ�P����y�ύ�ڵ�C��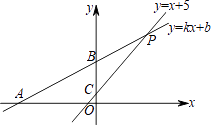
��1����ֱ��y=kx+b�Ľ���ʽ��
��2�����PBC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڼ���һ������ʽ��ƽ��ʱ���õ���ȷ���m2��10mn+���������һ�����īˮ��Ⱦ����һ��Ӧ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=![]() x2��
x2��![]() x��
x��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
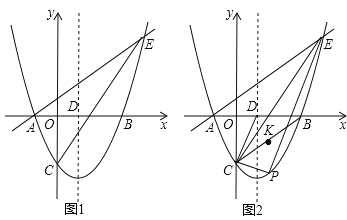
��1����ֱ��AE�Ľ���ʽ��
��2����PΪֱ��CE�·��������ϵ�һ�㣬����PC��PE������PCE��������ʱ������CD��CB����K���߶�CB���е㣬��M��CP�ϵ�һ�㣬��N��CD�ϵ�һ�㣬��KM+MN+NK����Сֵ��
��3����G���߶�CE���е㣬��������y=![]() x2��
x2��![]() x��
x��![]() ��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ����FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������Ʒÿ����4 kg��������Ʒÿ����7 kg�����м�����Ʒx����������Ʒy��������76 kg.
(1)�г�����x��y�Ķ�Ԫһ�η��̣�
(2)��x��12����y��_______��
(3)��������Ʒ��8�����������Ʒ��_______����
(4)д������������x��y��ȫ�������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������һ����ֱ�ĵ�·������������������г���A�ص�B�����Ҽݳ���B�ص�A�������Ƿֱ��Բ�ͬ���ٶ�������ʻ����֪���ȳ���6���Ӻ����Ҳų��������������������ס������˵ľ���y��ǧ�ף���׳�����ʱ��x���֣�֮��Ĺ�ϵ��ͼ��ʾ�����ҵ����յ�Aʱ������ ���ӵ����յ�B��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
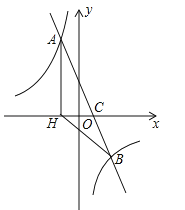
����Ŀ����ͼ����ƽ��ֱ������ϵ����һ�κ���y=ax+b��a��0����ͼ���뷴��������![]() ��k��0����ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC=
��k��0����ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC=![]() ��cos��ACH=
��cos��ACH=![]() ����B��������4��n��
����B��������4��n��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������BCH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬ�У�AB=8cm��BC=6cm��AC=7cm���ع���B��ֱ���۵������Σ�ʹ��C����AB�ߵĵ�E�����ۺ�ΪBD�����AED���ܳ�Ϊ �� 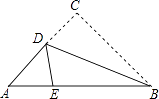
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com