解:①△ABC为直角三角形,理由如下:
连接AC,BC,

∵A(-

,0),B(2,0),C(0,1),
∴OA=

,OB=2,OC=1,
∴AB=OA+OB=

,即AB
2=

,
在Rt△AOC中,根据勾股定理得:AC
2=AO
2+OC
2=

+1=

,
在Rt△BOC中,根据勾股定理得:BC
2=BO
2+OC
2=4+1=5,
∴AC
2+BC
2=

+5=

=AB
2,
∴△ABC为直角三角形;
②A是弧CD的中点,理由为:
∵直径BA⊥弦CD,
∴A为

的中点;
③如上图所示:
当过N的直线l在x轴上边与圆M相切时,圆心M到直线l的距离d=r,
∵AB=

,
∴AM=r=

,
∴d=

,即m=

;
当过N的直线l在x轴下边与圆M相切时,圆心M到直线l的距离d=r,
∵AB=

,
∴AM=r=

,
∴d=

,即m=-

,
则当直线l与⊙M有公共点时,m的取值范围为-

≤m≤

;
④在y轴上存在点P,使得四边形APBC是梯形,
过点B作BP
1∥AC,交y轴于点P
1,
∴∠ACP
1=∠BP
1C,∠CAO=∠OBP
1,
∴△AOC∽△BOP
1,
∴

=
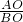
,即OP
1=

=4,
∴P
1坐标为(0,-4);
过点A作AP
2∥BC,交y轴于点P
2,
∴∠AP
2O=∠BCO,∠OAP
2=∠OBC,
∴△BOC∽△AOP
2,
∴

=

,即OP
2=

=

,
∴P
2坐标为(0,-

).
则在y轴上存在点P(0,-4)或(0,-

),使得四边形APBC是梯形.
分析:①三角形ABC为直角三角形,理由为:连接AC,BC,由A,B及C的坐标,得出OA,OB,及OC的值,在直角三角形AOC中,由OA及OC的长,利用勾股定理求出AC的长,在直角三角形BOC中,由OC及OB的长,利用勾股定理求出BC的长,同时由OA+OB求出AB的长,利用勾股定理的逆定理即可判断出三角形ABC为直角三角形;
②点A为弧CD的中点,理由为:由x轴与y轴垂直,得到直径BA与弦CD垂直,利用垂径定理可得出A为弧CD的中点;
③过y轴上一点N(0,m)作y轴的垂线l,当直线l在x轴上方与圆M相切时,根据圆心到切线的距离d=r,由直径AB的长求出半径r的长,可得出d的值,即为相切时N的纵坐标m的值;当直线l在x轴下方与圆M相切时,同理可得出相切时N的纵坐标m的值,当直线l在两切线之间时,直线与圆相交,符合题意,故得出直线l与圆M有公共点时m的范围;
④在y轴上存在点P,使得四边形APBC是梯形,此时满足题意的P有两个,一个是过B作BP
1与AC平行,与y轴交于P
1,根据两直线平行,得到两对内错角相等,根据两对对应角相等的两三角形相似,可得出三角形AOC与三角形BOP
1相似,由相似得比例,将OA,OB及OC的长代入求出OP
1的长,确定出P
1的坐标;另一个为过A作AP
2平行于BC,与y轴交于P
2,同理得出P
2的坐标,综上,得到所有满足题意的P的坐标.
点评:此题考查了直线与圆的位置关系,涉及的知识有:勾股定理及逆定理,垂径定理,平行线的性质,相似三角形的判定与性质,是一道综合性较强的题,第三小问抓住直线l与圆M相切时的特殊情况是求出m范围的关键.第四小问运用了分类讨论的思想,求出的P有两解,注意不要漏解.

 如图:平面直角坐标系中,已知A(-
如图:平面直角坐标系中,已知A(- ,0),B(2,0),C(0,1),△ABC的外接圆圆心为M,⊙M交y轴的负半轴于D.
,0),B(2,0),C(0,1),△ABC的外接圆圆心为M,⊙M交y轴的负半轴于D.
 ,0),B(2,0),C(0,1),
,0),B(2,0),C(0,1), ,OB=2,OC=1,
,OB=2,OC=1, ,即AB2=
,即AB2= ,
, +1=
+1= ,
, +5=
+5= =AB2,
=AB2, 的中点;
的中点; ,
, ,
, ,即m=
,即m= ;
; ,
, ,
, ,即m=-
,即m=- ,
, ≤m≤
≤m≤ ;
; =
=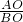 ,即OP1=
,即OP1= =4,
=4, =
= ,即OP2=
,即OP2= =
= ,
, ).
). ),使得四边形APBC是梯形.
),使得四边形APBC是梯形.

 =2
=2
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.