
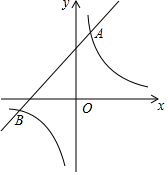
 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,且A点的橫坐标为1.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,且A点的橫坐标为1.分析 (1)将x=1代入y2=$\frac{6}{x}$求得点A坐标,再将点A坐标代入y1=x+m求得m的值,据此可得答案;
(2)联立两函数解析式得到方程组,解之得出点A、B的坐标,结合函数图象可得答案;
(3)先求得点C的坐标,再利用割补法求解可得答案.
解答 解:(1)在y2=$\frac{6}{x}$中当x=1时,y=6,即A(1,6),
将点A(1,6)代入y1=x+m,得:1+m=6,
解得m=5,
则一次函数解析式为y1=x+5;
(2)解$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=x+5}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{y=-1}\end{array}\right.$,
则点A(1,6)、点B(-6,-1),
由图象可知y1>y2时-6<x<0或x>1;
(3)当x=3时,y=$\frac{6}{3}$=2,
则点C(3,2),
如图,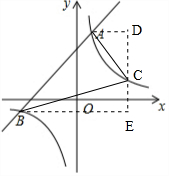
则AD=2、CD=4、BE=9、CE=3,
∴S△ABC=S梯形ABED-S△BCE-S△ACD
=$\frac{1}{2}$×(2+9)×7-$\frac{1}{2}$×9×3$\frac{1}{2}$×2×4
=21.
点评 本题考查了一次函数与反比例函数的交点问题,熟知用待定系数法求一次函数及反比例函数的解析式及三角形的面积公式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
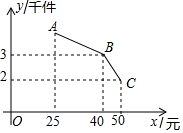 今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).
今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com