Question

16．如图，将边长为4cm的正方形纸片ABCD沿EF折叠（点E、F分别在边AB、CD上），使点B落在AD边上的中点M处，点C落在点N处，MN与CD交于点P，连接EP
（1）求△AEM的周长；
（2）判断线段EP、AE、DP之间的数量关系，并说明理由．

Answer 1

分析 （1）由折叠知BE=EM．AE+EM+AM=AE+EB+AM=AB+AM．根据边长及中点易求周长；
（2）首先取EP的中点G，连接MG，可得在梯形AEPD中，MG为中位线，在Rt△EMP中，MG为斜边EP的中线，继而求得答案．

解答 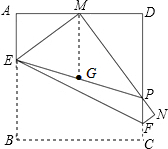解：（1）由折叠知BE=EM，∠B=∠EMP=90°．
△AEM的周长=AE+EM+AM=AE+EB+AM=AB+AM．
∵AB=4，M是AD中点，
∴△AEM的周长=4+2=6（cm）；

（2）EP=AE+DP．
理由：取EP的中点G，连接MG，
则在梯形AEPD中，MG为中位线，
∴MG=$\frac{1}{2}$（AE+PD），
在Rt△EMP中，MG为斜边EP的中线，
∴MG=$\frac{1}{2}$EP，
∴EP=AE+DP．

点评 此题考查了折叠的性质、梯形的性质、正方形的性质以及直角三角形的性质．注意准确作出辅助线是解此题的关键．