
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 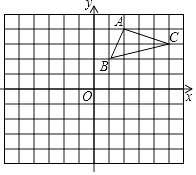
(1)①画出△ABC关于x轴对称的△A1B1C1 .
②画出△ABC绕原点O旋转180°后的△A2B2C2 , 并写出A2、B2、C2的坐标
(2)假设每个正方形网格的边长为1,求△A1B1C1的面积.
【答案】
(1)解:①如图,△A1B1C1为所作
②如图,△A2B2C2为所作,A2、B2、C2的坐标分别为(﹣2,﹣4),(﹣1,﹣2),(5,4)
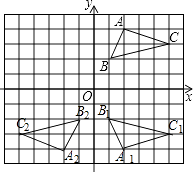
(2)解:△A1B1C1的面积=2×4﹣ ![]() ×2×1﹣
×2×1﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×4×1=
×4×1= ![]()
【解析】(1)先利用关于x轴对称的点的坐标特征写出A1、B1、C1的坐标,然后描点即可得到△A1B1C1;先利用关于原点对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可得到△A2B2C2;(2)利用矩形的面积分别减去三个三角形的面积.
【考点精析】解答此题的关键在于理解作轴对称图形的相关知识,掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据: ![]() =1.414,
=1.414, ![]() =1.732)
=1.732)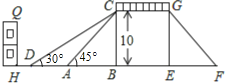
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点. 
(1)求∠D的度数;
(2)求证:AC2=ADCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= ![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
(1)如图①,当点E在射线CB上时,E点坐标为;
(2)当△CBD是等边三角形时,旋转角a的度数是(a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com