
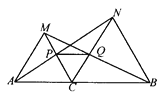
【题目】已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连结AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
【答案】见解析
【解析】试题分析:首先证明△ACN≌△MCB可得∠ANC=∠MBC,再证明△PCN≌△QCB可得PC=QC,再有∠MCN=60°可得△PCQ是等边三角形,进而得到∠PQC=60°,可证明PQ∥AB.
试题解析:∵△ACM和△BCN都是正三角形,
∴∠ACM=∠BCN=60°,AC=CM,BC=CN.
∵点C在线段AB上,
∴∠ACM=∠BCN=∠MCN=60°.
∴∠ACM+∠MCN=∠BCN+∠MCN=120°.
即∠NCA=∠BCM=120°.
∵在△ACN和△MCB中,
 ,
,
∴△ACN≌△MCB(SAS),
∴∠ANC=∠MBC,
∵在△PCN和△QCB中,
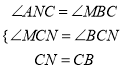 ,
,
∴△PCN≌△QCB(AAS),
∴PC=QC,
∵∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠PQC=60°,
∴∠PQC=∠QCB,
∴PQ∥AB.


科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2,过点B作BH⊥y轴于点H,连接 AH.
(1)求一次函数和反比例函数的解析式;(2)求△ABH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
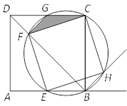
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°,CD为高,CE平分∠BCD,且∠ACD:∠BCD=1:2,那么CE是AB边上的中线对吗?说明理由.
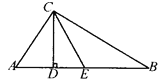
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
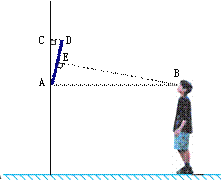
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
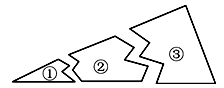
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
12
【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
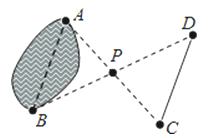
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com