
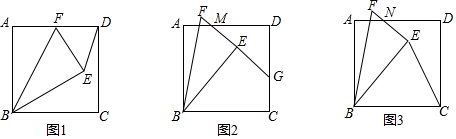
分析 (1)如图1中,作EH⊥BC于H,EM⊥CD于M.则四边形EMCH是矩形.想办法证明EM垂直平分CD即可解决问题;
(2)如图2中,连接BM、BG.由△BMA≌△BME,△BGE≌△BGC,推出AM=EM═DM=3,EG=CG,设EG=CG=x,则DG=6-x.在Rt△DMG中,根据MG2=DG2+DM2,列出方程即可解决问题;
(3)如图3中,连接BN,延长FE交CD于G,连接BG.只要证明∠ECD=∠GCB,推出tan∠GBC=tan∠ECD=$\frac{1}{2}$,推出$\frac{CG}{BC}$=$\frac{1}{2}$,推出CG=3,由CD=6,可得CG=DG=3,设AN=EN=y,则DN=6-y,在Rt△DNG中,利用勾股定理求出y即可解决问题;
解答 解:(1)如图1中,作EH⊥BC于H,EM⊥CD于M.则四边形EMCH是矩形.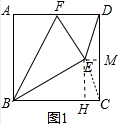
∵四边形ABCD是正方形,
∴BA=BC,∠ABC=∠BCD=90°,
∵BC=BE,
∴AB=BE,
在Rt△BFA和Rt△BFE中,
$\left\{\begin{array}{l}{BF=BF}\\{BA=BE}\end{array}\right.$,
∴Rt△BFA≌△Rt△BFE,
∴∠ABF=∠EBF=30°,
∵∠ABC=90°,
∴∠EBC=30°,
∴EH=MC=$\frac{1}{2}$BE=$\frac{1}{2}$CD,
∴DM=CM,∵EM⊥CD,
∴ED=EC,
∵∠BCE=$\frac{1}{2}$(180°-30°)=75°,
∴∠EDC=∠ECD=15°.
(2)如图2中,连接BM、BG.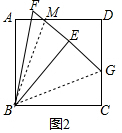
由(1)可知△BMA≌△BME,△BGE≌△BGC,
∴AM=EM═DM=3,EG=CG,设EG=CG=x,则DG=6-x.
在Rt△DMG中,∵MG2=DG2+DM2,
∴(3+x)2=(6-x)2+32,
∴x=2,
∴EG=2.
(3)如图3中,连接BN,延长FE交CD于G,连接BG.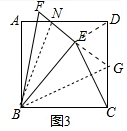
易知AN=NE,EG=CG,
∵BE=BC,
∴BG垂直平分CE,
∴∠ECG+∠BCG=90°,∵∠GBC+∠ECB=90°,
∴∠ECD=∠GCB,
∴tan∠GBC=tan∠ECD=$\frac{1}{2}$,
∴$\frac{CG}{BC}$=$\frac{1}{2}$,
∴CG=3,
∵CD=6,
∴CG=DG=3,设AN=EN=y,则DN=6-y,
在Rt△DNG中,(6-y)2+32=(3+y)2,
解得y=2,
∴AN=NE=2,DN=4,NG=5,
∴S△DNE=$\frac{2}{5}$•S△DNG=$\frac{2}{5}$×3×4=$\frac{24}{5}$.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
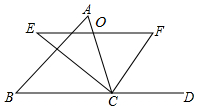 如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).
如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
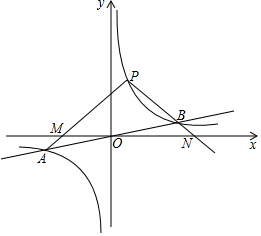 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com