
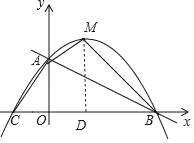
【题目】如图,在直角坐标系中,已知直线y=-![]() x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,联结AM、BM,求四边形AOBM的面积.

【答案】(1)y=-![]() (2)31
(2)31
【解析】分析:(1)先利用一次函数解析式确定A(0,4),B(8,0),再设交点式y=a(x+2)(x-8),然后把A点坐标代入求出a即可得到抛物线解析式;
(2)先利用配方法得到y=-![]() (x-3)2+
(x-3)2+![]() ,则M(3,
,则M(3,![]() ),作MD⊥x轴于D,如图,然后根据梯形面积公式和三角形面积公式,利用四边形AOBM的面积=S梯形AODM+S△BDM进行计算即可.
),作MD⊥x轴于D,如图,然后根据梯形面积公式和三角形面积公式,利用四边形AOBM的面积=S梯形AODM+S△BDM进行计算即可.
详解:
(1)当x=0时,y=-![]() x+4=4,则A(0,4),
x+4=4,则A(0,4),
当y=0时,-![]() x+4=0,解得x=8,则B(8,0),
x+4=0,解得x=8,则B(8,0),
设抛物线解析式为y=a(x+2)(x﹣8),
把A(0,4)代入得a2(﹣8)=4,解得x=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x+2)(x﹣8),
(x+2)(x﹣8),
即y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)∵y=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,
,
∴M(3,![]() ),
),
作MD⊥x轴于D,如图,
四边形AOBM的面积=S梯形AODM+S△BDM
=![]() ×(4+
×(4+![]() )×3+
)×3+![]() ×5×
×5×![]()
=31.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() ﹣(﹣2
﹣(﹣2![]() )+(﹣3
)+(﹣3![]() )﹣(+4
)﹣(+4![]() )
)
(2)(﹣![]() ﹣
﹣![]() +
+![]() )×(﹣24)
)×(﹣24)
(3)(﹣3)÷![]() ×
×![]() ×(﹣15)
×(﹣15)
(4)﹣14+|(﹣2)3﹣10|﹣(﹣3)÷(﹣1)2017.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某智能手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
已知A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共90部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.

解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 、
、![]() 轴于点A、B两点,OA=5,∠OAB=60°.
轴于点A、B两点,OA=5,∠OAB=60°.
(1)如图1,求直线AB的解析式;
(2)如图2,点P为直线AB上一点,连接OP,点D在OA延长线上,分别过点P、D作OA、OP的平行线,两平行线交于点C,连接AC,设AD=m,△ABC的面积为S,求S与m的函数关系式;
(3)如图3,在(2)的条件下,在PA上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE的周长等于22,求S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com