
分析 (1)设购买一个A品牌足球需x元,购买一个B品牌足球需(x+30)元.接下来,依据购买A品牌足球数量是购买B品牌足球数量的2倍列方程求解即可;
(2)设此次可购买a个B品牌的足球,则购进A品牌足球(50-a)个,接下来依据总费用不超过3260元列不等式求解即可.
解答 解:(1)设购买一个A品牌足球需x元,购买一个B品牌足球需(x+30)元.
根据题意得:$\frac{2500}{x}$=$\frac{2000}{x+30}$×2.
解得:x=50.
经检验x=50是原方程的解.则x+30=80.
答:购买一个A品牌的足球需要50元,购买一个B品牌的足球需80元.
(2)设此次可购买a个B品牌的足球,则购进A品牌足球(50-a)个.
由题意得:50(1+8%)(50-a)+80×0.9a≤3260.
解得;a≤31$\frac{1}{9}$.
∵a是整数,
∴a最大可取31.
答:这所中学此次最多可购买31个B品牌的足球.
点评 本题主要考查的是分式方程的应用、一元一次不等式的应用,根据题意列出方程和不等式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+2y=8}\\{2x+5y=10}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+2y=10}\\{x+5y=8}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=2}\\{2x+5y=8}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
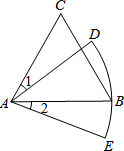 如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).
如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 组号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
| 频数 | 14 | 11 | 12 | 13 | ■ | 13 | 12 | 10 |
| A. | 14 | B. | 15 | C. | 0.14 | D. | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
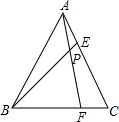 △ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.
△ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com