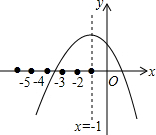练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．小颖用计算器探索方程ax2+bx+c=0的根，作出如图所示的图象，并求得一个近似根x=-3.4，则方程的另一个近似根（精确到0.1）为（　　）
    A．4.4B．3.4C．2.4D．1.4

    分析 根据一元二次方程的一个近似根，得到抛物线与x轴的一个交点，根据抛物线的对称轴，求出另一个交点坐标，得到方程的另一个近似根．

    解答 解：∵抛物线与x轴的一个交点为（-3.4，0），又抛物线的对称轴为：x=-1，
    ∴另一个交点坐标为：（1.4，0），
    则方程的另一个近似根为1.4，
    故选：D．

    点评 本题考查的是用图象法求一元二次方程的近似根，掌握二次函数的对称性和抛物线与x轴的交点与一元二次方程的解的关系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷（解析版） 题型：填空题

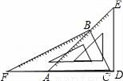
    如图，把一副常用的三角板如图所示拼在一起，那么图中∠ABF=______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知△ABC的三边分别是x，y，z，①以$\sqrt{x}$，$\sqrt{y}$，$\sqrt{z}$为三边的三角形一定存在；②以x2，y2，z2为三边的三角形一定存在；③以$\frac{1}{2}$（x+y），$\frac{1}{2}$（y+z），$\frac{1}{2}$（x+z）为三边的三角形一定存在；④以|x-y|+1，|y-z|+1，|z-x|+1为三边的三角形一定存在；上述四个结论中，正确的是①③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

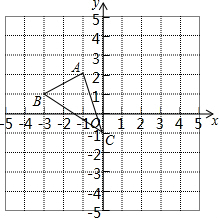    7．如图，图形中每一小格正方形的边长为1，已知△ABC
    （1）AC的长等于$\sqrt{10}$．（结果保留根号）
    （2）将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是（1，2）；
    （3）画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1，并写出A点对应点A1的坐标？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

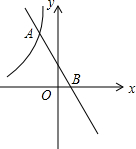    14．如图，一次函数y2=-2x+b（b为常数）的图象与反比例函数y1=$\frac{k}{x}$（k为常数，且k≠0）的图象交于A，B两点，且点A的坐标为（-1，4）．当y1＜y2时，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在平行四边形ABCD中，AB=5，BC=12，对角线交于点O，∠BAD的平分线交BC于E、交BD于F，分别过顶点B、D作AE的垂线，垂足为G、H，连接OG、OH．
    （1）补全图形；
    （2）求证：OG=OH；
    （3）若OG⊥OH，直接写出∠OAF的正切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

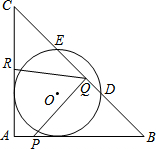    11．如图，在△ABC中，∠A=90°，AB=AC=12cm，半径为4cm的⊙O与AB、AC两边都相切，与BC交于点D、E．点P从点A出发，沿着边AB向终点B运动，点Q从点B出发，沿着边BC向终点C运动，点R从点C出发，沿着边CA向终点A运动．已知点P、Q、R同时出发，运动速度分别是1cm/s、xcm/s、1.5cm/s，运动时间为ts．
    （1）求证：BD=CE；
    （2）若x=3，当△PBQ∽△QCR时，求t的值；
    （3）设△PBQ关于直线PQ对称的图形是△PB'Q，求当t和x分别为何值时，点B′与圆心O恰好重合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

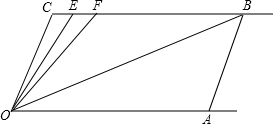    8．如图，已知直线CB∥OA，∠C=100°，点E、F在CB边上，且满足∠FOB=∠AOB，OE平分∠COF．
    （1）求∠EOB的度数；
    （2）若平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，请找出变化的规律；若不变，求出这个比值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．小开到一早点摊买东西，下面是他和卖早点阿姨的对话．
    小开说：“我买这种包子8个，这种油条5根．”
    阿姨说：“一共13元6角．”
    付款后，小开说：“阿姨，这两根油条不要了，换3个一样的包子吧．”
    阿姨说：“可以，但还需补交2元钱．”
    从他们的对话中你能知道这种包子、油条的单价吗？

    查看答案和解析>>

    同步练习册答案