
【题目】在平面直角坐标系xOy中,直线y=2x+m与y轴交于点A,与直线y=﹣x+4交于点B(3,n),P为直线y=﹣x+4上一点.
(1)求m,n的值;
(2)在平面直角坐标系系xOy中画直线y=2x+m和直线y=﹣x+4;
(3)当线段AP最短时,求点P的坐标.
【答案】(1)m=﹣5;(2)详见解析;(3)![]()
【解析】
(1)首先把点B(3,n)代入直线y=﹣x+4得出n的值,再进一步代入直线y=2x+m求得m的值即可;(2)根据两点法画一次函数图形即可;(3)过点A作直y=﹣x+4的垂线,垂足为P,进一步利用等腰直角三角形的性质和(1)中与y轴交点的坐标特征解决问题.
解:(1)∵点B(3,n)在直线上y=﹣x+4,
∴n=1,B(3,1)
∵点B(3,1)在直线上y=2x+m上,
∴m=﹣5.
(2)在坐标系中画出y=2x﹣5,y=﹣x+4,如图①,

(3)过点A作直线y=﹣x+4的垂线,垂足为P,如图②
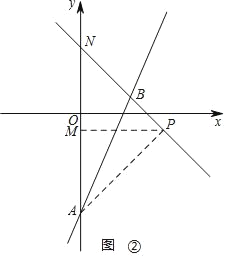 ,
,
此时线段AP最短.
∴∠APN=90°,
∵直线y=﹣x+4与y轴交点N(0,4),直线y=2x﹣5与y轴交点A(0,﹣5),
∴AN=9,∠ANP=45°,
∴AM=PM=![]() ,
,
∴OM=![]()
∴![]() .
.


科目:初中数学 来源: 题型:
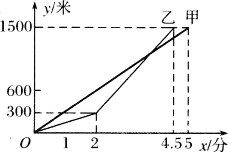
【题目】甲、乙两人进行1500米比赛,在比赛时,两人所跑的路程y(米)与所用的时间x(分)间的函数关系如图所示,解答下列问题:
(1)求甲的速度等于多少米/分;
(2)当乙到终点时,甲距离终点有多远;
(3)乙在距终点多远处追上了甲.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF;
②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.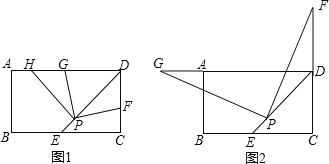
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .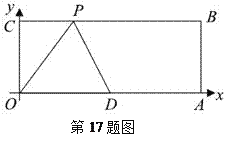
查看答案和解析>>
科目:初中数学 来源: 题型:
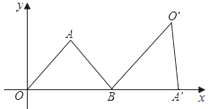
【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
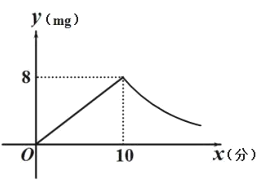
【题目】为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 ![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 成正比例;燃烧后,
成正比例;燃烧后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃完,此时教室内每立方米空气含药量为
分钟燃完,此时教室内每立方米空气含药量为![]() .根据以上信息解答下列问题:
.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后 ![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当每立方米空气中的含药量低于![]() 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于![]() 的持续时间超过
的持续时间超过![]() 分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月27日,军运会闭幕,军运村对武汉市民正式销售,此楼盘开盘均价20000元/ m2,为了加快资金回笼,房地产开发商决定将价格下调10%对外销售,并在此基础上再给予以下三种优惠方案供客户选择:
①一次性付款可以再打9.8折销售;
②一次性付款,不享受折上折,但可送两年物业管理费(物业管理费是每平方米每月3元),再一次性送30000元装修费;
③如果先付总房款的一半,可送一年的物业管理费,再一次性送10000元装修费,但是一年后必须一次性付清余下的房款.(注:该年将钱存入银行,银行的年利率为3%)
(1)若所购房屋面积为a m2,分别用含a的代数式表示这三种方案的买房费用。
(2)某客户准备购买其中一套100 m2的房子,如果该客户有能力一次性付清所有房费,请问他该选择哪种付款方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com