
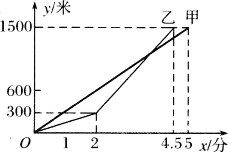
【题目】甲、乙两人进行1500米比赛,在比赛时,两人所跑的路程y(米)与所用的时间x(分)间的函数关系如图所示,解答下列问题:
(1)求甲的速度等于多少米/分;
(2)当乙到终点时,甲距离终点有多远;
(3)乙在距终点多远处追上了甲.
【答案】(1)300米/分;
(2)150m;
(3)400m
【解析】
(1)根据图像即可求解;
(2)利用待定系数法确定函数关系式分别求出甲乙的函数解析式即可求解;
(3)令两函数相等求出交点坐标,即可得到答案.
(1)甲的速度为![]() =300米/分;
=300米/分;
(2)甲的所跑的路程y(米)与所用的时间x(分)间的函数关系为y1=300x;
x=4.5时,y1=1350,
1500-1350=150m
∴当乙到终点时,甲距离终点有150m;
(2)
设乙在2≤x≤4.5时,函数解析式为y2=kx+b,
把(2,300)和(4.5,1500)代入得![]()
解得k=480,b=-660
∴2≤x≤4.5, y2=480x-660
令y1= y2,即300x=480x-660
解得x=3![]()
x=3![]() ,y1=1100,
,y1=1100,
1500-1100=400,
故乙在距终点400m追上甲.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )

A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.
与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.

(1)直接写出A、B两点的坐标:A(______,_____)、B(_____,_____);
(2)在AB上找一点P,当PC+PO最小时,在AC上找一点Q使得PQ+![]() 最小,求Q点坐标;
最小,求Q点坐标;
(3)在(2)的条件下,平面内能否找到一点K,使得点A、C、P、K构成的四边形是平行四边形,若能,直接写出K点坐标,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借助下面的材料,
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离:|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离:|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A点B在数轴上分别表示有理数a,b,那么点A、点B之间的距离可表示为|a﹣b|.
问题:如图,数轴上A,B两点对应的有理数分别为﹣8和12,点P从点O出发,以每秒1个单位长度的速度沿数轴负方向运动,点Q同时从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)求经过2秒后,数轴点P、Q分别表示的数;
(2)当t=3时,求PQ的值;
(3)在运动过程中是否存在时间t使AP=![]() AB,若存在,请求出此时t的值,若不存在,请说明理由.
AB,若存在,请求出此时t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念
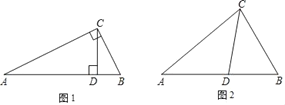
(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.
概念应用
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )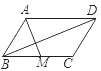
A. 30B. 36C. 54D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+m与y轴交于点A,与直线y=﹣x+4交于点B(3,n),P为直线y=﹣x+4上一点.
(1)求m,n的值;
(2)在平面直角坐标系系xOy中画直线y=2x+m和直线y=﹣x+4;
(3)当线段AP最短时,求点P的坐标.
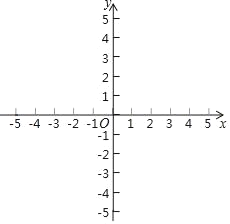
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com