
【题目】实数a, b在数轴上对应的点如图所示;
![]()
(1)如图:比较大小:a________b,a—b________0,a + b_______0;
(2)如图:化简(去绝对值号)|b|= _______,|a+1| =__________.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】数轴上![]() ,
,![]() ,
,![]() 所对应的点分别为点
所对应的点分别为点![]() ,点
,点![]() ,点
,点![]() 。若点
。若点![]() 到点
到点![]() 的距离表示为
的距离表示为![]() ,点
,点![]() 到点
到点![]() 的距离表示为
的距离表示为![]() 。我们有
。我们有![]() ,
,![]() .
.

(1)点![]() ,点
,点![]() ,点
,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,
,![]() ,
,![]() .且
.且![]() ,直接写出
,直接写出![]() 的值 。
的值 。
(2)在(1)的条件下,两只电子蚂蚁甲,乙分别从![]() ,
,![]() 两点出发向右运动,甲的速度为
两点出发向右运动,甲的速度为![]() 个单位每秒,乙的速度为
个单位每秒,乙的速度为![]() 个单位每秒。求经过几秒,点
个单位每秒。求经过几秒,点![]() 与两只蚂蚁的距离和等于
与两只蚂蚁的距离和等于![]() .
.
(3)在(1)(2)的条件下,电子蚂蚁乙运动到点![]() 后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点
后立即以原速返回,到达自己的出发点后停止运动,电子蚂蚁甲运动至点![]() 后也以原速返回,到达自己的出发点后又折返向点
后也以原速返回,到达自己的出发点后又折返向点![]() 运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。
运动,当电子蚂蚁乙停止运动时,电子蚂蚁甲随之停止运动。求运动时间为多少时,两只蚂蚁相遇。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红有5张写着以下数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1) 从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是_________
(2) 从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是_________
(3) 从中取出除0以外的其他4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使运算结果为24(注:每个数字只能用一次,如:23×[1-(-2)],请另外写出两种符合要求的运算式子:_________________ _________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米)+10,-9,+7,-15,+6,-14,+4,-2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0, ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形A′BC′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的.点O′在x轴的正半轴上,点B的坐标为(1,3).
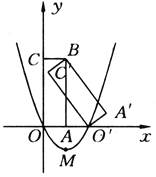
(1)如果二次函数y=ax2+bx+c(a≠0)的图象经过O,O′两点,且图象顶点M的纵坐标为-l,求这个二次函数的解析式;
(2)在(1)中求出的二次函数图象对称轴的右侧,是否存在点P,使得△POM为直角三角形?若存在,求出点P的坐标和△POM的面积;若不存在,请说明理由;
(3)求边C′O′所在直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com