
【题目】如图,在数轴上点A,点B,点C表示的数分别为﹣2,1,6.
![]()
(1)线段AB的长度为 个单位长度,线段AC的长度为 个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为 个单位长度,点P在数轴上表示的数为 ;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
【答案】(1)3;8;(2)(3﹣t)或(t﹣3);﹣2+t;(3)x=3;M在数轴上表示的数是10.
【解析】
(1)根据两点间的距离公式可求线段AB的长度,线段AC的长度;
(2)先根据路程=速度×时间求出点P运动的路程,再分点P在点B的左边和右边两种情况求解;
(3)根据等量关系点M、N两点间的距离为13个单位长度列出方程求解即可.
(1)线段AB的长度为1﹣(﹣2)=3个单位长度,线段AC的长度为6﹣(﹣2)=8个单位长度;
(2)线段BP的长为:当t≤3时,BP=3﹣t;当t>3时,BP=t﹣3,点P在数轴上表示的数为﹣2+t;
(3)∵AC=8<13,∴M、N相遇后再走13个单位长度,依题意有:
4x+3x﹣8=13
解得:x=3.
此时点M在数轴上表示的数是﹣2+4×3=10.
故答案为:(1)3;8;(2)(3﹣t)或(t﹣3);﹣2+t.


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,以O为顶点、OB为一边画∠BOC,然后再分别画出∠AOC与∠BOC的平分线OM、ON.
(1)在图1中,射线OC在∠AOB的内部.
①若锐角∠BOC=30°,则∠MON= °;
②若锐角∠BOC=n°,则∠MON= °.
(2)在图2中,射线OC在∠AOB的外部,且∠BOC为任意锐角,求∠MON的度数.
(3)在(2)中,“∠BOC为任意锐角”改为“∠BOC为任意钝角”,其余条件不变,(图3),求∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.
(1)篮球和排球单价各是多少元?
(2)若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?
(3)如果购买这两种球刚好用去520元,问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
(1)如图,在平面内有不共线的3个点A,B,C.
(a)作直线AB,射线AC,线段BC;
(b)延长BC到点D,使CD=BC,连接AD;
(c)作线段AB的中点E,连接CE;
(d)测量线段CE和AD的长度,直接写出二者之间的数量关系_______.

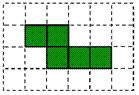
(2) 有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
注意:只需添加一个符合要求的正方形,并用阴影表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题: 如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.
小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 . 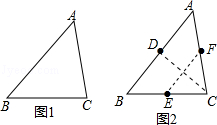
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A,B为数轴上两点,AB=15,且OA:OB=2
(1)A,B对应的数分别为 , .
(2)点A,B分别以2个单位/秒和5个单位/秒的速度相向而行,则几秒后A,B相距1个单位长度?
(3)点AB以(2)中的速度同时向右运动,点P从原点O以4个单位秒的速度向右运动,是否存在常数m,使得3AP+2PB﹣mOP为定值?若存在,请求出m值以及这个定值;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
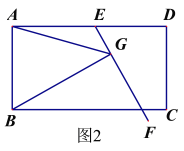
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C是直角,AB=6cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的D处,则AC边扫过的图形众人阴影部分的面积是 . 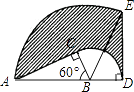
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com