
【题目】已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE∥AC,且DE=AC,若AC=2,AD=4,求四边形ACEB的周长.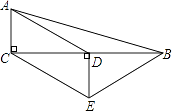
【答案】解:∵DE∥AC,且DE=AC
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△ACD中,由勾股定理得CD= ![]() =2
=2 ![]() .
.
∵D是BC的中点,
∴BC=2CD=4 ![]() .
.
在△ABC中,∠ACB=90°,由勾股定理得AB= ![]() .
.
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+2 ![]() .
.
【解析】首先判断出四边形ACED是平行四边形.根据平行四边形的性质得出DE=AC=2.在Rt△ACD中,由勾股定理得CD的长,根据中点定义得出BC的长,在△ABC中,∠ACB=90°,由勾股定理得AB的长,根据中垂线定理得出EB=EC=4,根据四边形周长的计算方法得出答案。


科目:初中数学 来源: 题型:
【题目】下列命题中不是真命题的是( )
A.对角线相等的平行四边形是矩形B.对角线互相垂直的四边形是菱形
C.平行四边形的对角线互相平分D.正方形的对角线互相垂直且相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.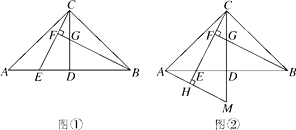
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() 为
为![]() 的中点,作
的中点,作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
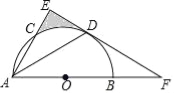
(1)求证:![]() 为半圆
为半圆![]() 的切线;
的切线;
(2)若![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过
的图象经过![]() 三点.
三点.
(1)求该二次函数的解析式;
(2)点![]() 是该二次函数图象上的一点,且满足
是该二次函数图象上的一点,且满足![]() (
(![]() 是坐标原点),求点
是坐标原点),求点![]() 的坐标;
的坐标;
(3)点![]() 是该二次函数图象上位于一象限上的一动点,连接
是该二次函数图象上位于一象限上的一动点,连接![]() 分别交
分别交![]() 轴与点
轴与点![]() 若
若![]() 的面积分别为
的面积分别为![]() 求
求![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com