
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).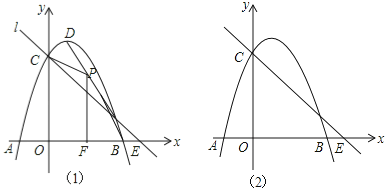
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
【答案】
(1)
【解答】解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),
当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线l的解析式为y=kx+b,
把C(0,3),E(4,0)分别代入得![]() ,解得
,解得 ,
,
∴直线l的解析式为y=![]() x+3;
x+3;
(2)
如图(1),当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),
设直线BD的解析式为y=mx+n,
把B(3,0),D(1,4)分别代入得![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=﹣2x+6,
则P(x,﹣2x+6),
∴S=![]() (﹣2x+6+3)x=﹣x2+
(﹣2x+6+3)x=﹣x2+![]() x(1≤x≤3),
x(1≤x≤3),
∵S=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;

(3)
存在.
如图2,设Q(t,0)(t>0),则M(t,![]() t+3),N(t,﹣t2+2t+3),
t+3),N(t,﹣t2+2t+3),
∴MN=|﹣t2+2t+3﹣(![]() t+3)|=|t2﹣
t+3)|=|t2﹣![]() t|,
t|,
CM=![]() =
=![]() t,
t,
∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,
而QN∥y轴,
∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,
∴∠M′CN=∠CNM,
∴∠M′CN=∠CNM′,
∴CM′=NM′,
∴NM=CM,
∴|t2﹣![]() t|=
t|=![]() t,
t,
当t2﹣![]() t=
t=![]() t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
t,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
当t2﹣![]() t=
t=![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,0),
,0),
综上所述,点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
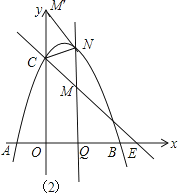
【解析】(1)先把抛物线解析式配成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先根据抛物线与x轴的交点问题求出B(3,0),再利用待定系数法求出直线BD的解析式为y=﹣2x+6,则P(x,﹣2x+6),然后根据梯形的面积公式可得S=﹣x2+![]() x(1≤x≤3),再利用而此函数的性质求S的最大值;
x(1≤x≤3),再利用而此函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则可表示出M(t,﹣![]() t+3),N(t,﹣t2+2t+3),利用两点间的距离公式得到MN=|t2﹣
t+3),N(t,﹣t2+2t+3),利用两点间的距离公式得到MN=|t2﹣![]() t|,CM=
t|,CM=![]() t,然后证明NM=CM得到|t2﹣
t,然后证明NM=CM得到|t2﹣![]() t|=
t|=![]() t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.
t,再解绝对值方程求满足条件的t的值,从而得到点Q的坐标.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲口袋中有三张完全相同的卡片,分别标有﹣1,1,2,乙口袋中有完全相同的卡片,分别标有﹣2,3,4,从这两个口袋中各随机取出一张卡片.
(1)用树状图或列表表示所有可能出现的结果;
(2)求两次取出卡片的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com