
【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( ) 
A.4
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
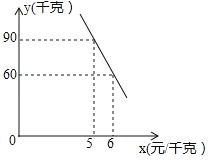
【题目】(12分)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:

(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF. 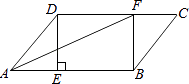
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
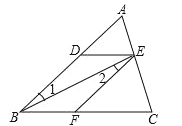
【题目】把下面的说理过程补充完整
已知:如图,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
证明:∵DE∥BC(已知)
∴∠ADE= ( )
∵∠ADE=∠EFC(已知)
∴ = ( )
∴DB∥EF ( )
∴∠1=∠2 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
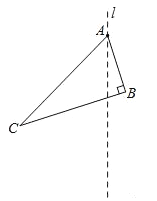
【题目】如图,已知Rt△ABC中,∠ABC=90°,经过点A的直线l与BC交于点F.
(1)请作出△ABC关于直线l轴对称的△ADE(A、B、C的对应点分别是A、D、E)
(2)连接CD,EB,在不添加其它辅助线的情况下,请你找出图中的一对全等三角形: ≌ ;
(3)证明(2)中的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小区规划在一个长80m,宽40m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地的其余部分种草,甬道的宽度为am.

(1)用含x的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC与BD相交于点O,下列结论中不正确的是( )
A. 当AD=DC时,四边形ABCD是菱形 B. 当AB2=OA2+OB2时,四边形ABCD是菱形
C. 当OA=OB时,四边形ABCD是矩形 D. 当∠ABD=∠CBD时,四边形ABCD是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级共有学生600人,为了解这些学生的视力情况,抽查了50名学生的视力,并对所得数据进行了整理,在得到的频数分布表中,数据在0.95~1.15这一组频率为0.3,则可估计该校七年级学生视力在0.95~1.15范围内的人数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com