
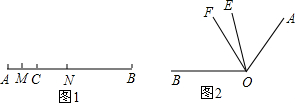
分析 (1)直接利用两点之间距离分别得出CN,MC的长进而得出答案;
(2)直接利用角平分线的性质以及结合已知角的关系求出答案.
解答 解:(1)∵M是AC的中点,AC=6,
∴MC=$\frac{1}{2}$AC=6×$\frac{1}{2}$=3,
又因为CN:NB=1:2,BC=15,
∴CN=15×$\frac{1}{3}$=5,
∴MN=MC+CN=3+5=8,
∴MN的长为8 cm;
(2)∵∠BOE=2∠AOE,∠AOB=∠BOE+∠AOE,
∴∠BOE=$\frac{2}{3}$∠AOB,
∵OF平分∠AOB,
∴∠BOF=$\frac{1}{2}$∠AOB,
∴∠EOF=∠BOE-∠BOF=$\frac{1}{6}$∠AOF,
∵∠EOF=20°,
∴∠AOB=120°.
点评 此题主要考查了角平分线的定义以及两点之间距离,正确把握相关定义是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )
如图,一张长方形纸片的长AD=4,宽AB=1.点E在边AD上,点F在BC边上,将四边形 ABFE沿直线EF翻折后,点B落在边AD的中点G处,则EG等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{17}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com