
����Ŀ����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺

��1����A��Ϊ��ת���ģ�����ABC�Ƶ�A˳ʱ����ת90��á�AB1C1��������AB1C1��
��2��������ABC��������ԭ��O�����ĶԳƵġ�A2B2C2��
��3��������C����x��ĶԳƵ�P������P����ƽ��x��xȡ����������λ���Ⱥ����ڡ�A2B2C2���ڲ�����ֱ��д��x��ֵ��
���𰸡���ͼ������.
��������
�����������1���������εĸ����㶼�Ƶ�A˳ʱ����ת90���õ���Ӧ�㣬˳�����Ӽ��ɣ�
��2��������ABC�ĸ��������ԭ������ĶԳƣ��ó�A2��B2��C2�����꣬���Ӹ��㣬���ɵ���A2B2C2��
��3����������C����x��ĶԳƵ�P���ٸ���ƽ�Ƶ����ʵõ�x��ֵ��
�����������1����ͼ���ң���A1B1C1��Ϊ����
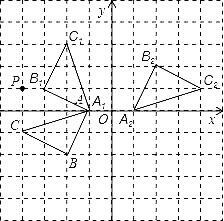
��2����ͼ���ң���A2B2C2��Ϊ����
��3��x��ֵΪ6��7��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy����������M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1��
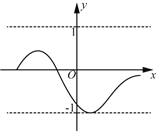
��1���ֱ��жϺ��� y=![]() ��x��0����y=x+1����4��x��2���Dz����н纯���������н纯��������߽�ֵ��
��x��0����y=x+1����4��x��2���Dz����н纯���������н纯��������߽�ֵ��
��2��������y=��x+1��a��x��b��b��a���ı߽�ֵ��2����������������ֵҲ��2����b��ȡֵ��Χ��
��3�������� y=x2����1��x��m��m��0����ͼ������ƽ��m����λ���õ��ĺ����ı߽�ֵ��t����m��ʲô��Χʱ������![]() ��t��1��
��t��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OABC��ƽ���ı��Σ��Խ���OB��y���������ϣ�λ�ڵ�һ���ĵ�A�͵ڶ����ĵ�C�ֱ���˫����![]() ��
��![]() ��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��![]() ������Ӱ���������
������Ӱ���������![]() ��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��
��k1+k2�����۵���AOC=90��ʱ��|k1|=|k2|������OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�������ȷ�Ľ����ǣ� ��

A���٢ڢ� B���ڢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F��
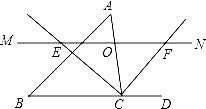
��1����CE=12��CF=5����OC�ij���
��2������O�ڱ�AC���˶�ʱ���ı���BCFE�������������ǣ���֤���������ǣ���˵�����ɣ�
��3������O�˶����δ����ҡ�ABC����ʲô����ʱ���ı���AECF�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı��ε������Խ��߳���8cm��16cm�������ƽ���ı��ε�һ�߳������ǣ�������
A. 3cm B. 4cm C. 8cm D. 12cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������11�֣�
A��B�������600ǧ�ף�һ��������A�ؿ�����ÿСʱ��ʻ80ǧ�ף�һ�п쳵��B�ؿ�����ÿСʱ��ʻ120ǧ�ף�����ͬʱ������
��1����������У����������Сʱ������
��2��������У�����Сʱ���������800ǧ����
��3��������ͬ����У��쳵���������棬����Сʱ�쳵��������
��4��������ͬ����У������ڿ쳵���棬����Сʱ���������760ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��LA��LB�ֱ��ʾA������B�ﳵ��ͬһ·����ʻ��·��y��ǧ�ף���ʱ��x��Сʱ���Ĺ�ϵ������ͼ�ش��������⣺

��1��B����ʱ��A��� ǧ�ף�
��2��B�ﳵһ��·�����г��������ϣ��������������õ�ʱ���� Сʱ��
��3��B������ Сʱ��A������
��4�����A���ߵ�·��y��ʱ��x�ĺ�����ϵʽ����д�����̣�
��5����B�����г����������ϣ����ֳ���ʱ���ٶ�������ʻ��A��B�϶�����ǰ��������ͼ�л������ּ��������B�ﳵ��ʻ������·��y��ʱ��x�ĺ���ͼ����ͼ�б�����������P�����ش�������P��B�ij�����O������ǧ�ף���д�����̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com