
【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(![]() )∠EAC与∠B相等吗?为什么?
)∠EAC与∠B相等吗?为什么?
(![]() )若
)若![]() ,
,![]() ,则
,则![]() = .
= .
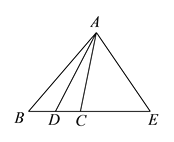
【答案】(1)见解析;(2)48°.
【解析】
(1)由于AD平分∠BAC,根据角平分线的概念可得∠BAD=∠CAD,再根据三角形的一个外角等于和它不相邻的两个内角和,结合已知条件可得∠EAC与∠B相等;
(2)若设∠CAD=x°,则∠E=3x°.根据(1)中的结论以及三角形的内角和定理及其推论列方程进行求解即可.
(1)相等.理由如下:
∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵∠EAD=∠EDA,
∴∠EAC=∠EAD﹣∠CAD.
=∠EDA﹣∠BAD.
=∠B;
(2)设∠CAD=x°,则∠E=3x°,由(1)知:∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.
在△EAD中,∵∠E+∠EAD+∠EDA=180°,∴3x+2(x+50)=180,解得:x=16,∴∠E=48°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
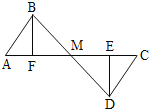
【题目】如图,E、F分别为线段AC上两个动点,且DE⊥AC于E,BF⊥AC于F,若AB=CD,AF=CE,BD交AC于M.说明:MB=MD,ME=MF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 . 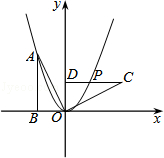
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )

A. 122°20′ B. 122°21′ C. 122°22′ D. 122°23′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是 ![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B.一组数据6,8,7,8,8,9,10的众数和中位数都是8
C.为了解全国中学生的心理健康情况,应该采用普查的方式
D.若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元. 
(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生在颁奖大会上得知该班获得奖励的情况如下表:
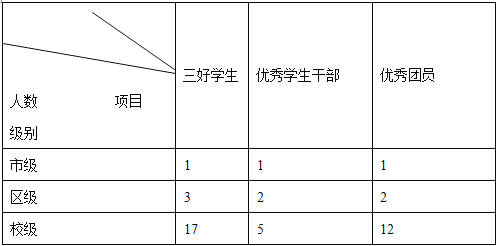
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A. 3项 B. 4项 C. 5项 D. 6项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com