
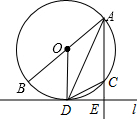
 如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.
如图所示,已知AB是⊙O的直径,弦AD是∠BAC的平分线,过点D作⊙O的切线l,且AC⊥DE,垂足为点E.分析 (1)连接BD,证得△ABD∽△ADE,根据相似三角形的性质即可证得结论;
(2)证得△ADE∽△DEC,根据相似三角形的性质得AC=2,根据勾股定理得出DC=2,然后证得△OAD≌△CAD,根据全等三角形的性质证得OA=AC=2=OD=DC,即可证得四边形ACDO是菱形.
解答 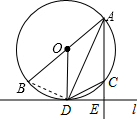 (1)证明:连接BD,
(1)证明:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AC⊥DE,
∴∠ADB=∠AED=90°,
∵∠BAD=∠EAD,
∴△ABD∽△ADE,
∴$\frac{AB}{AD}$=$\frac{AD}{AE}$,
∴AD2=AB•AE;
(2)解:四边形ACDO是菱形,
∵DE=$\sqrt{3}$,CE=1,
∴DC=$\sqrt{D{E}^{2}+C{E}^{2}}$=2,
∵直线l是⊙O的切线,切点是D,
∴∠CDE=∠DAC,
∵∠AED=∠DEC,
∴△ADE∽△DEC,
∴$\frac{DE}{CE}$=$\frac{AE}{DE}$,即$\frac{\sqrt{3}}{1}$=$\frac{AE}{\sqrt{3}}$,
∴AE=3,
∴AC=AE-CE=3-1=2,
∴AC=CD=2,
∴∠DAC=∠ADC,
∵∠BAD=∠DAC,∠BAD=∠ODA,
∴∠OAD=∠ODA=∠DAC=∠ADC,
在△OAD和△CAD中,
$\left\{\begin{array}{l}{∠OAD=∠CAD}\\{AD=AD}\\{∠ODA=∠CDA}\end{array}\right.$
∴△OAD≌△CAD(ASA),
∴OA=AC=2=OD=DC,
∴四边形ACDO是菱形.
点评 本题考查了切线的性质,圆周角定理,相似三角形的判定和性质,全等三角形的判定和性质等,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
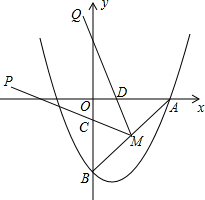 如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.
如图,抛物线y=ax2-2ax-4交x轴的正半轴于点A,交y轴于点B,且OA=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学生的视力状况受到社会的普遍关注,某校为了解学生的视力情况,对本校学生的视力情况进行了抽样调查,并对调查结果进行了整理,制成了所示的统计图标(不完整),x表示视力情况.根据所提供的信息,解答下列问题:
学生的视力状况受到社会的普遍关注,某校为了解学生的视力情况,对本校学生的视力情况进行了抽样调查,并对调查结果进行了整理,制成了所示的统计图标(不完整),x表示视力情况.根据所提供的信息,解答下列问题:| 分组 | 视力情况 | 频数 | 频率 |
| A | x<4.1 | 20 | 0.10 |
| B | 4.1≤x<4.5 | 70 | 0.35 |
| C | 4.5≤x<4.9 | 50 | 0.25 |
| D | x≥4.9 | 60 | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
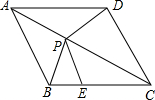 如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.
如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com