
 如图,圆E是三角形ABC的外接圆,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
如图,圆E是三角形ABC的外接圆,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.分析 (1)如图1中,连接EB、EC.由BC=OB+OC=5,∠BEC=2∠BC=90°,可知EB=EC=$\frac{5\sqrt{2}}{2}$.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.利用勾股定理求出点A、B、C三点坐标,利用待定系数法即可解决问题.
(3)①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.②当PA⊥OA时,有一个点P满足条件.③当PO⊥OA时,有两个点P满足条件.
解答 解:(1)如图1中,连接EB、EC.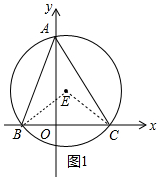
∵BC=OB+OC=5,∠BEC=2∠BC=90°,
∴EB=EC=$\frac{5\sqrt{2}}{2}$,
∴⊙E的直径为$5\sqrt{2}$.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.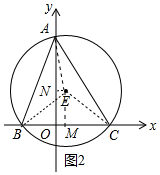
在Rt△EMC中,EM=ON=$\sqrt{E{C}^{2}-C{M}^{2}}$=$\sqrt{(\frac{5\sqrt{2}}{2})^{2}+(\frac{5}{2})^{2}}$=$\frac{5}{2}$,OM=NE=OC-CM=$\frac{1}{2}$,
在Rt△EN中,AN=$\sqrt{A{E}^{2}-E{N}^{2}}$=$\sqrt{(\frac{5\sqrt{2}}{2})^{2}-(\frac{1}{2})^{2}}$=$\frac{7}{2}$,
∴OA=AN+ON=6,
∴A(0,6),B(-2,0),C(3,0),
设抛物线的解析式为y=a(x+2)(x-3),把(0,6)的坐标代入得a=-1,
∴抛物线的解析式为y=-x2+x+6.
(3)如图3中,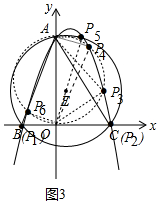
①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.
②当PA⊥OA时,有一个点P满足条件.
③当PO⊥OA时,有两个点P满足条件.
所以满足条件的点P有6个.
点评 本题考查二次函数综合题、圆的有关知识、勾股定理、待定系数法等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用直径所对的圆周角是直角寻找直角,所以中考压轴题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
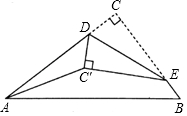 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )
如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,点D、E分别在AC、BC上.现将△DCE沿DE翻折,使点C落在点C'处.连接AC',则AC'长度的最小值.( )| A. | 不存在 | B. | 等于1cm | C. | 等于2 cm | D. | 等于2.5 cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com