
��ͼ����֪���κ�����ͼ����A��6��0����B����2��0���͵�C��0����8����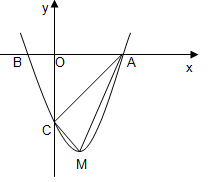
��1����ö��κ����Ľ���ʽ��
��2����ö��κ���ͼ��Ķ���ΪM������KΪx���ϵĶ��㣬����KCM���ܳ���Сʱ����K������Ϊ�� ����
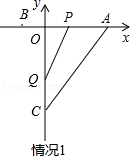
��3������AC����������P��Qͬʱ�ӵ�O���������е�P��ÿ��3����λ���ȵ��ٶ�������OAC��O��A��C��·���˶�����Q��ÿ��8����λ���ȵ��ٶ�������OCA��O��C��A��·���˶�����P��Q��������ʱ�����Ƕ�ֹͣ�˶�����P��Qͬʱ�ӵ�O����t��ʱ����OPQ�����ΪS��
������P��Q�������˶������У��Ƿ����PQ��OC�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
�������S����t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
����S0�Ǣ��к���S�����ֵ��ֱ��д��S0��ֵ��
��1��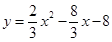 ����2����
����2����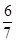 ��0������3���ٲ����ڣ����ɼ������������
��0������3���ٲ����ڣ����ɼ������������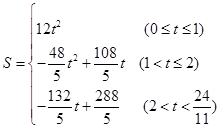 ����
����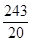 ��
��
���������������1��������֪����x���������������;�����һ�����ý���ʽ����κ����Ľ���ʽ���ɣ�
��2�����ȸ���������õĺ����Ľ���ʽȷ���������꣬Ȼ����õ�C����x��ĶԳƵ������C�䣬�Ӷ����ֱ��C��M�Ľ���ʽ�������x��Ľ������꼴�ɣ�
��3����3�������DE��OC����ʱ��D��EӦ�ֱ����߶�OA��CA�ϣ�������������t��ȡֵ��Χ��Ȼ�����ƽ���߷��߶γɱ��������������ʱt��ֵ��Ȼ��t��ֵ�Ƿ���ϴ��������t��ȡֵ��Χ��������������t��ֵ���������ֵ����������ϣ���ô��˵��������������t��
�ڱ���Ҫ����������������ۣ���E��OC�ϣ�D��OA�ϣ�����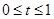 ʱ����ʱS=
ʱ����ʱS=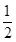 OE•OD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OE•OD���ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
��E��CA�ϣ�D��OA�ϣ����� ʱ����ʱS=
ʱ����ʱS=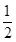 OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
OD��E��������꣮�ɴ˿ɵó�����S��t�ĺ�����ϵʽ��
��E��D����CA��ʱ������ ����ʱ�õ�ʱ�䣬��ʱS=S��AOE��S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ��
����ʱ�õ�ʱ�䣬��ʱS=S��AOE��S��AOD���ɴ˿ɵó�S��t�ĺ�����ϵʽ��
�����������ɵó���ͬ��t��ȡֵ��Χ�ڣ������IJ�ͬ����ʽ��
�۸��ݢڵĺ������ɵó�S�����ֵ��
�����������1������κ����Ľ���ʽΪ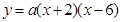 ����ͼ����㣨0����8������
����ͼ����㣨0����8������ ������κ����Ľ���ʽΪ
������κ����Ľ���ʽΪ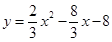 ��
��
��2����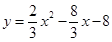 =
=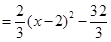 �����M��������2��
�����M������Ϊ��2��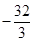 �����ߵ�C������Ϊ��0��
�����ߵ�C������Ϊ��0�� �������C����x��ԳƵĵ�C�������Ϊ��0��8������ֱ��C��M�Ľ���ʽΪ��
�������C����x��ԳƵĵ�C�������Ϊ��0��8������ֱ��C��M�Ľ���ʽΪ��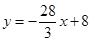 ����
���� ����
����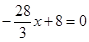 ����ã�
����ã�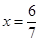 �����K������Ϊ��
�����K��������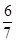 ��0����
��0����
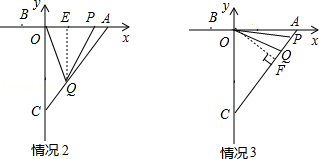
��3���ٲ�����PQ��OC��
��PQ��OC�����P��Q�ֱ����߶�OA��CA�ϣ���ʱ�� ����PQ��OC�����APQ�ס�AOC����
����PQ��OC�����APQ�ס�AOC����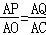 ����AP=
����AP=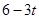 ��AQ=
��AQ=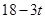 ����
����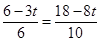 ����
����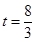 ����
����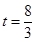 ��2������
��2������ �������PQ��OC��
�������PQ��OC��
�ڷ�����������£�
���1��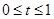
S=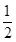 OP•OQ=
OP•OQ=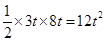 ��
��
���2��
��QE��OA������ΪE��S=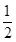 OP•EQ=
OP•EQ=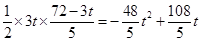 ��
��
���3�� ��
��
��OF��AC������ΪF����OF=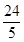 ��S=
��S=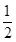 QP•OF=
QP•OF=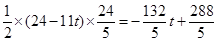 ��
��
��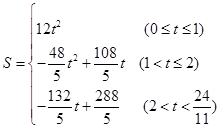 ��
��
�۵�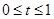 ʱ��
ʱ�� �����������ֵ��12��
�����������ֵ��12��
�� ʱ��
ʱ��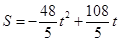 �����������ֵ��
�����������ֵ��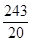 ��
��
�� ��
��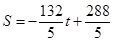 �����������ֵΪ
�����������ֵΪ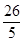 ��
��
��S0��ֵΪ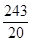 ��
��
���㣺���κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������y=2x2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��1��д����A��B��CΪ����������������
��2������E��0��6������x��ƽ�е�ֱ��l1���������ཻ��M��N���㣨��M�ڵ�N����ࣩ����MNΪһ�ߣ��������ϵ���һ��PΪ��һ������ƽ���ı��Σ���ƽ���ı��ε����Ϊ8ʱ�������P�����ꣻ
��3������D��m��0��������m��1������x�ᴹֱ��ֱ��l2����һ��Q����Q�ڵ�һ���ޣ���ʹ����Q��D��BΪ����������κ���B��C��OΪ��������������ƣ����߶�QD�ij����ú�m�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�������ߵĽ���ʽ�к�����ĸϵ��ʱ������ϵ���е���ĸȡֵ�IJ�ͬ�������ߵĶ�������Ҳ�������仯.���磺��������y=x2��2mx+m2+2m��1����y=(x��m)2+2m��1�ڣ�
���������߶�������Ϊ��m��2m��1������x=m��,y=2m��1��.
��m��ֵ�仯ʱ��x��y��ֵҲ��֮�仯�����y��ֵҲ��xֵ�ı仯���仯.
���۴���ܣ���y=2x��1��.�ɼ�������mȡ�κ�ʵ���������߶����������y�ͺ�����x�������ϵʽ��y=2x��1��
���������Ķ������ṩ�ķ�����ȷ���㣨��2m, m��1������ĺ�����ϵʽΪ_______.
(2)�����Ķ������ṩ�ķ�����ȷ�������� �����������y�������x֮��Ĺ�ϵʽ.
�����������y�������x֮��Ĺ�ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��˾������һ�ֽ�����Ʒ���г����ܵ��ձ黶ӭ��ÿ����ڹ��ڡ������г���ȫ�����꣬�ù�˾�������Ϊ6ǧ�������ڹ����г����ۣ�ƽ��ÿ����Ʒ������y1��Ԫ���������������x��ǧ�����Ĺ�ϵΪ�� ���ڹ������ۣ�ƽ��ÿ����Ʒ������y2��Ԫ����������������t��ǧ�����Ĺ�ϵΪ��
���ڹ������ۣ�ƽ��ÿ����Ʒ������y2��Ԫ����������������t��ǧ�����Ĺ�ϵΪ��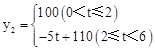
��1����x�Ĵ���ʽ��ʾtΪ��t�� ����0��x��4ʱ�� y2��x�ĺ�����ϵΪy2�� ���� ��x�� ʱ��y2��100��
��2����ÿ��ù�˾�������ֽ�����Ʒ��������w��ǧԪ������ڵ���������x��ǧ�����ĺ�����ϵʽ����ָ��x��ȡֵ��Χ��
��3���ù�˾ÿ����ڡ��������������Ϊ����ʱ����ʹ��˾ÿ���������������ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�������������ִ�ѧ����ҵ�������������ķ�����Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�ƣ����۹����з��֣�ÿ��������y(��)�����۵���x(Ԫ)֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����y����10x��500.
��1��������ÿ�»������Ϊw(Ԫ)�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������6�֣�
��2�����������Ҫÿ�»��2 000Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ����3�֣�
��3����۲��Ź涨�����ֻ���̨�Ƶ����۵��۲��ø���32Ԫ�����������Ҫÿ�»�õ�������2 000Ԫ����ô��ÿ�µijɱ�������Ҫ����Ԫ��(�ɱ������ۡ�������) ��3�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
����С������12�֣���ͼ���ı���OABCΪֱ�����Σ�A��4��0����B��3��4����C��0��4������M��O������ÿ��2����λ���ȵ��ٶ���A�˶�����N��Bͬʱ��������ÿ��1����λ���ȵ��ٶ���C�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������N��NP��ֱx���ڵ�P������AC��NP��Q������MQ��
��1���� ����M��N���ܵ����յ㣻
��2�����AQM�����S���˶�ʱ��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ����tΪ��ֵʱ��S��ֵ���
��3���Ƿ���ڵ�M��ʹ�á�AQMΪֱ�������Σ������ڣ������M�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�������������ÿ������Ϊ40Ԫ����ߣ��г����鷢�֣�����ÿ��50Ԫ�ļ۸����ۣ�ƽ��ÿ������90��������ÿ���1Ԫ��ƽ��ÿ���������3����
��1��ƽ��ÿ���������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵʽΪ�� ����
��2�����������ƽ��ÿ�����������W��Ԫ�������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��
��3����۲��Ź涨ÿ���ۼ۲��ø���55Ԫ����ÿ����ߵ����ۼ�Ϊ����Ԫʱ�����Ի�����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������ ��
�� �ύ�ڵ�
�ύ�ڵ� .
.
��1��ƽ�Ƹ�������ʹ�侭���� �͵�
�͵� ��2,0������ƽ�ƺ�������߽���ʽ��
��2,0������ƽ�ƺ�������߽���ʽ��
��2����������ߵĶԳ����루1����ƽ�ƺ�������߶Գ���֮��ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ֱ������ϵxOy�У����κ���y=x2+��2k��1��x+k+1��ͼ����x���ཻ��O��A���㣮
��1����������κ����Ľ���ʽ��
��2�������������ߵĶԳ����ұߵ�ͼ������һ��B��ʹ��AOB���������6�����B�����ꣻ
��3�����ڣ�2���еĵ�B���ڴ����������Ƿ���ڵ�P��ʹ��POB=90�㣿�����ڣ������P�����꣬�������POB��������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com