
分析 (1)因式分解法求解可得;
(2)配方法求解可得.
解答 解:(1)∵x(x+6)=0,
∴x=0或x+6=0,
解得:x=0或x=-6;
(2)x2-5x=-3,
x2-5x+$\frac{25}{4}$=-3+$\frac{25}{4}$,即(x-$\frac{5}{2}$)2=$\frac{13}{4}$,
∴x-$\frac{5}{2}$=±$\frac{\sqrt{13}}{2}$,
即x1=$\frac{5-\sqrt{13}}{2}$,x2=$\frac{5+\sqrt{13}}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:解答题
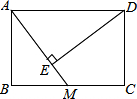 已知:如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E.
已知:如图,在矩形ABCD中,AB=4,BC=6,M是边BC的中点,DE⊥AM,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠ACD=90°.
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠ACD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
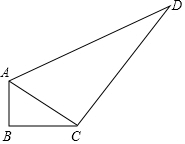
 如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com