
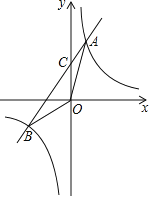
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是
的图象交于A、B两点,且点A的横坐标是2,点B的纵坐标是![]() 求:
求:
![]() 一次函数的解析式;
一次函数的解析式;
![]() 的面积;
的面积;
![]() 直接写出使反比例函数的值大于一次函数的值的x的取值范围.
直接写出使反比例函数的值大于一次函数的值的x的取值范围.
【答案】(1)一次函数的解析式为![]() .(2)6;(3)
.(2)6;(3)![]() 或
或![]() .
.
【解析】分析:
(1)根据已知条件先求得点A、B的坐标,然后将所得坐标代入一次函数的解析式列出关于k、b的方程组,解方程组求得k、b的值即可得到一次函数的解析式;
(2)由(1)中所得一次函数的解析式求得点C的坐标,这样结合点A、B的坐标由S△AOB=S△AOC+S△BOC即可求得△AOB的面积了;
(3)由点A、B的坐标结合函数图象即可得到反比例函数的函数值大于一次函数的函数值时对应的x的取值范围.
详解:
![]() 令反比例函数
令反比例函数![]() ,
,![]() ,则
,则![]() ,
,
∴点A的坐标为![]() ;
;
反比例函数![]() 中
中![]() ,则
,则![]() ,解得:
,解得:![]() ,
,
∴点B的坐标为![]() .
.
∵一次函数过A、B两点,
∴![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为![]() ;
;
![]() 设直线AB与y轴交于C,
设直线AB与y轴交于C,
令![]() 中
中![]() ,则
,则![]() ,
,
∴点C的坐标为![]() ,
,
∴S△AOB=S△AOC+S△BOC=![]() ;
;
![]() 观察函数图象发现:
观察函数图象发现:
当![]() 或
或![]() 时,反比例函数图象在一次函数图象上方,
时,反比例函数图象在一次函数图象上方,
∴反比例函数的函数值大于一次函数的函数值时x的取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
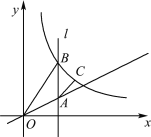
【题目】如图,已知点A是一次函数y=![]() x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=
x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=![]() (x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
(x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质
的图象与性质
(1)函数![]() 的自变量x的取值范围是___;
的自变量x的取值范围是___;
(2)下列四个函数图象中,函数![]() 的图象大致是___;
的图象大致是___;
A.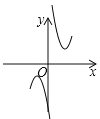 B.
B.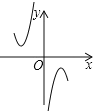 C.
C.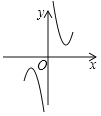 D.
D.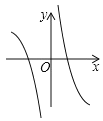
(3)对于函数![]() ,求当
,求当![]() 时,y的取值范围。
时,y的取值范围。
请将下面求解此问题的过程补充完整:
解:∵x>0
∴![]()
=![]()
∵![]()
∴y=____.
(拓展应用)
(4)若函数![]() ,求y的取值范围.
,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,由若干个棱长完全相同的小正方体搭成一个几何体.

(1)请画出这个几何体的主视图和左视图(作图必须用黑色墨水描黑);
(2)如果保持主视图和左视图不变,那么这个几何体最多可以再添加 个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() ,
, ![]() 交于点
交于点![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求![]() 的面积;
的面积;
(4)在直线![]() 上存在异于点
上存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= ;
(2)你能否由此归纳出一般规律(x﹣1)(xn+xn﹣1+……+x+1)= ;
(3)根据以上规律求32018+32017+32016+…32+3+1的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知 AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=2,AE =3,AD=7,求线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新个税法于2018年9月1日全面实施,工资、薪金所得基本减除费用标准由3500元提高至5000元,并按新的税率表计算纳税:
序号 | 税前每月工资的各部分 | 税率 |
1 | 不超过5000元部分 | 0% |
2 | 超过5000元至8000元的部分 | 3% |
3 | 超过8000元至17000元的部分 | 10% |
4 | 超过17000元至30000元的部分 | 20% |
5 | 超过30000元至40000元的部分 | 25% |
6 | 超过40000元至60000元的部分 | 30% |
7 | 超过60000元至80000元的部分 | 35% |
8 | 超过80000元的部分 | 45% |
(1)在新个税法实施后,小王没扣税前某月工资7800元,他这个月应交税 元;
(2)在新个税法实施后,若小李没扣税前某月工资x元![]() ,他这个月交税y元,则y= ;
,他这个月交税y元,则y= ;
(3)在新个税法实施后,一企业某月把奖金放在工资里发放(奖金跟工资一起扣税),该企业员工小刘这个月领取了工资加奖金(税后)26410元.已知小刘没扣税前工资为a元![]() ,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
,若工资和奖金分两次发放(工资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com