
����Ŀ��ij��ѧ�½���һ���IJ�Ľ�ѧ¥��ÿ��¥��10����ң������ⶰ��ѧ¥����4���ţ������������Ŵ�С��ͬ���������Ŵ�СҲ��ͬ����ȫ����У���4���Ž����˲��ԣ���ͬʱ����һ�����ź���������ʱ��2�����ڿ���ͨ��560��ѧ������ͬʱ����һ�����ź�һ������ʱ��4�����ڿ���ͨ��800��ѧ����
��1����ƽ��ÿ����һ�����ź�һ�����Ÿ�����ͨ��������ѧ����
��2������з��֣����ֽ������ʱ����ѧ��ӵ�������ŵ�Ч�ʽ�����20%����ȫ���涨���ڽ��������ȫ¥��ѧ��Ӧ��5������ͨ����4���Ű�ȫ���룬�����ⶰ��ѧ��¥ÿ����������45��ѧ�����ʣ��ý�ѧ¥�������4�����Ƿ���ϰ�ȫ�涨����˵�����ɣ�
���𰸡�
��1���⣺��һ������ƽ��ÿ����ͨ��x��ѧ����һ������ƽ��ÿ����ͨ��y��ѧ���������⣬��
![]() ����ã�
����ã� ![]() ��
��
��һ������ƽ��ÿ����ͨ��120��ѧ����һ������ƽ��ÿ����ͨ��80��ѧ��
��2���⣺�����⣬��
����ѧ����45��10��4=1800��
1800ѧ��ͨ����ʱ��Ϊ��1800�£�120+80����0.8��2= ![]() ���ӣ�
���ӣ�
��5�� ![]() ��
��
��ý�ѧ¥�������4���Ų����ϰ�ȫ�涨
����������1����һ������ƽ��ÿ����ͨ��x��ѧ����һ������ƽ��ÿ����ͨ��y��ѧ������������ͨ����ѧ����+����ͨ����ѧ����=ͨ�����������������������⼴�ɣ���2���ȼ�����������������������µ�λʱ����ͨ���������Ϳ������ʱ�䣬����5���ӽ��бȽϾÿ��Եó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������70ǧ�ף��״�A�س�����ÿСʱ��15ǧ�ף��Ҵ�B�س�����ÿСʱ��20ǧ�ף�
(1)������ͬʱ������������У�����Сʱ����������
(2)������ǰ�����ں�����ͬʱͬ����У���Сʱ���ҳ�����10ǧ�ף�
(3)������ͬʱ������������У���Сʱ���������10ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ı��ι��ɣ�
![]() ��
��![]() ��
��![]() ������
������
�����������⣺
��1����������ĸ�ʽ��д��![]() =�� ����
=�� ����
��2����n���������������![]() =�� ����
=�� ����
��3������Ӧ�ã����㣺![]() ��
��
��4����չӦ��1���ⷽ�̣�![]() =2016
=2016
��5����չӦ��2�����㣺![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
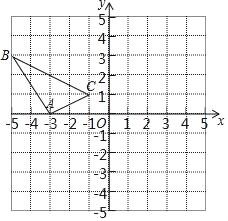
����Ŀ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У�������ͼ��ʾ��ƽ��ֱ������ϵ��ABC�Ǹ�������Σ������������ߵĽ����ϣ�
��1��������ABC����ԭ��O�����ĶԳƵġ�A1B1C1���ٰѡ�A1B1C1����ƽ��4����λ���ȵõ���A2B2C2��
��2����A2B2C2���ABC�Ƿ����ij������ĶԳƣ����ǣ�ֱ��д���Գ����ĵ����ꣻ�����ǣ���˵������.
���𰸡���1����ͼ����������2����0��2��.
��������
��1���������ĶԳƺ�ƽ�����ʷֱ������任��������Ķ�Ӧ�㣬��˳�����ӿɵã�
��2���������ĶԳƵĸ�����жϣ�
��1����ͼ��ʾ����A1B1C1�͡�A2B2C2��Ϊ����
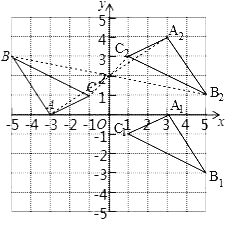
��2����ͼ��֪����A2B2C2���ABC���ڵ㣨0��2�������ĶԳƣ�
�㾦�����⿼�������ĶԳ���ͼ��ƽ����ͼ�������������ĶԳƵ����ʺ�ƽ�Ƶ������ǽ����Ĺؼ�. ���ĶԳƵ����ʣ��ٹ������ĶԳƵ�����ͼ���ܹ���ȫ�غϣ��ڹ������ĶԳƵ�����ͼ�Σ���Ӧ������߶������Գ����ģ����ұ��Գ�����ƽ��.
�����͡������
��������
22
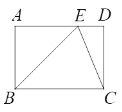
����Ŀ����ͼ���ھ���ABCD�У���E��AD�ϣ���ECƽ�֡�BED.
��1����BEC�Ƿ�Ϊ����������?֤����Ľ���.
��2����֪AB=1����ABE=45������BC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㷨ͳ�ڡ����й��Ŵ���ѧ�������������ҹ�������ѧ�ҳ̴�λ���ڡ��㷨ͳ�ڡ��м��أ��������⾮�����������۲�֮������4�ߣ����������۲�֮������1�ߣ�������������Σ���
���ģ��������Ӳ�ˮ����ȣ�����������۳����ȷݣ���������4�ߣ�����������۳��ĵȷݣ���������1�ߣ���������������Ƕ��ٳߣ���
�辮��Ϊx�ߣ����������з��̣���ȷ���ǣ�������

A. 3��x+4��=4��x+1�� B. 3x+4=4x+1
C. 3��x��4��=4��x��1�� D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��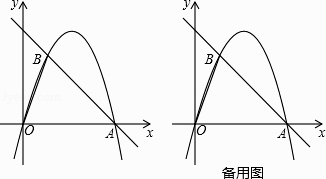
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM//OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR//MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ͺ��͵��϶�����������A�ص�B��ȼ����ʻ��ȼ�ͷ���76Ԫ����A�ص�B���õ���ʻ�������26Ԫ����֪ÿ��ʻ1ǧ�ף���ȼ�ͷ��ñȴ��õ���ö�0.5Ԫ��
��1����ÿ��ʻ1ǧ�״��õ�ķ��ã�
��2����Ҫʹ��A�ص�B���͵�����ʻ������͡�����úϼƲ�����39Ԫ���������õ���ʻ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵΪ�˱���������������A��B�����ͺŵ���ˮ�����豸��8̨������ͬʱ������ͬ�ɷֵ���ˮ��������A��2̨��B��3̨��54����A��4̨��B��2̨��68��Ԫ��
��1�����A�͡�B����ˮ�����豸�ĵ��ۣ�
��2������ʵ��һ̨A���豸һ���¿ɴ�����ˮ220�֣�һ̨B���豸һ���¿ɴ�����ˮ190�֣��������ҵÿ�µ���ˮ������������1565�֣�����Ϊ����ҵ���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com