
【题目】A、B两地相距70千米,甲从A地出发,每小时行15千米,乙从B地出发,每小时行20千米.
(1)若两人同时出发,相向而行,则经过几小时两人相遇?
(2)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10千米?
(3)若两人同时出发,相向而行,则几小时后两人相距10千米?
【答案】(1)经过2小时两人相遇;
(2)经过16小时,乙超过甲10千米
(3)![]() 小时或
小时或![]() 小时后两人相距10千米.
小时后两人相距10千米.
【解析】
(1)设两人同时出发相向而行,需经过x小时两人相遇,由甲走的路程+乙走的路程=70千米建立方程求出其解即可;
(2)设甲在前,乙在后,两人同时同向而行,a小时后乙超过甲10千米,由乙走的路程=甲走的路程+70+10建立方程求出其解即可;
(3)设两人同时出发相向而行,需b小时两人相距16千米,根据相遇前与相遇后分别建立方程求出其解即可.
(1)设经过x小时两人相遇,
15x+20x=70,解得x=2.
答:经过2小时两人相遇;
(2)设经过a小时,乙超过甲10千米,
20a=15a+70+10,
解得a=16.
答:经过16小时,乙超过甲10千米;
(3)设b小时后两人相距10千米,
|15b+20b–70|=10,
解得b1=![]() ,b2=
,b2=![]() .
.
答:![]() 小时或
小时或![]() 小时后两人相距10千米.
小时后两人相距10千米.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】某学校的复印任务原来由甲复印社承包,其收费y(元)与复印页数x(页)的关系如下表:
x(页) | 100 | 200 | 400 | 1000 | … |
y(元) | 40 | 80 | 160 | 400 | … |
(1)根据表格信息写出y与x之间的关系式;
(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费.乙复印社每月收费y(元)与复印页数x(页)之间的关系式为_______________;
(3)若学校每月复印页数在1200页左右,应选择哪个复印社?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 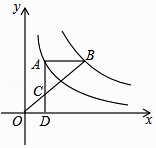
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D是AC上的一点,在BC上取一点E,使BE=CD,连接AE交BD于点P,在BD的延长线上取一点Q,使AP=PQ,连接AQ、CQ,点G为PQ的中点,DG=PE,若CQ=![]() ,则BQ=________________.
,则BQ=________________.
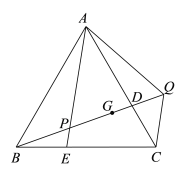
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C坐标分别是(8,0),(0,4),反比例函数y= ![]() (x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( )
(x>0)的图象过对角线的交点P并且与AB、BC分别交于D、E两点,连接OD、OE、DE,则△ODE的面积为( ) 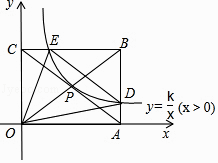
A.14
B.12
C.15
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C. 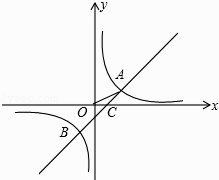
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
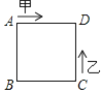
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com