
【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM= ![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.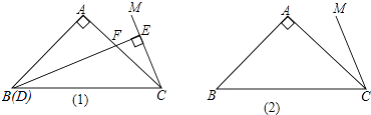
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
【答案】
(1)解:如图(1),延长BA,CM交点N,

∵∠A=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵∠ACM= ![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BCM=67.5°,
∴∠BNC=67.5°=∠BCM,
∴BC=BN,
∵BE⊥CE,
∴∠ABE=22.5°,CN=2CE,
∴∠ABE=∠ACM=22.5°,
在△BAF和△CAN中, 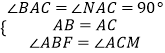 ,
,
∴△BAF≌△CAN(ASA),
∴BF=CN,
∴BF=2CE
(2)解:保持上述关系;BF=2CE;
证明如下:
作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,
如图(2)所示:
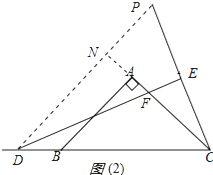
∵DE⊥PC,∠ECD=67.5,
∴∠EDC=22.5°,
∴∠PDE=∠EDC,∠NDC=45°,
∴∠DPC=67.5°,
∴PD=CD,
∴PE=EC,
∴PC=2CE,
∵∠NDC=45°,∠NCD=45°,
∴∠NCD=∠NDC,∠DNC=90°,
∴ND=NC且∠DNC=∠PNC,
在△DNF和△PNC中, 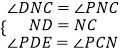 ,
,
∴△DNF≌△PNC(ASA),
∴DF=PC,
∴DF=2CE.
【解析】(1)延长BA,CM交点N,先证明BC=BN,得出CN=2CE,再证明△BAF≌△CAN,得出对应边相等BF=CN,即可得出结论;
(2)作∠PDE=22.5,交CE的延长线于P点,交CA的延长线于N,先证明PD=CD,得出PC=2CE,再证明△DNF≌△PNC,得出对应边相等DF=PC,即可得出结论.


科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形边长都是1.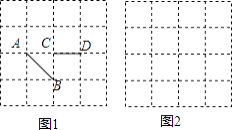
(1)图1中已知线段AB、CD,画线段EF,使它与AB、CD组成轴对称图形(要求:画出一个即可);
(2)在图2中画出一个以格点为端点长为 ![]() 的线段.
的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P位于x轴下方,距离x轴5个单位,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
A.(5,-3) B.(3,-5) C.(-5,3) D.(-3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
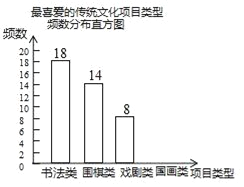
【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
(1)频数分布表中a=_____,b=_____;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的周长为11cm,其中一边长为3cm,则该等腰三角形的底长为( )
A. 3cm或5cm B. 3cm或4cm C. 3cm D. 5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com