
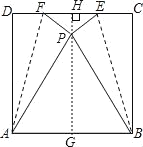
【题目】如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是_____.

【答案】![]()
【解析】
过P作PH⊥DC于H,交AB于G,由正方形的性质得到AD=AB=BC=DC=2;∠D=∠C=90°;再根据折叠的性质有PA=PB=2,∠FPA=∠EPB=90°,可判断△PAB为等边三角形,利用等边三角形的性质得到∠APB=60°,![]() ,于是∠EPF=120°,PH=HG﹣PG=2﹣
,于是∠EPF=120°,PH=HG﹣PG=2﹣![]() ,得∠HEP=30°,然后根据含30°的直角三角形三边可求出HE,得到EF,最后利用三角形的面积公式计算即可.
,得∠HEP=30°,然后根据含30°的直角三角形三边可求出HE,得到EF,最后利用三角形的面积公式计算即可.
解:过P作PH⊥DC于H,交AB于G,如图,
则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=![]() AB=
AB=![]() ,
,
∴∠EPF=120°,PH=HG﹣PG=2﹣![]() ,
,
∴∠HEP=30°,
∴HE=![]() PH=
PH=![]() (2﹣
(2﹣![]() )=2
)=2![]() ﹣3,
﹣3,
∴EF=2HE=4![]() ﹣6,
﹣6,
∴△EPF的面积=![]() FEPH=
FEPH=![]() (2﹣
(2﹣![]() )(4
)(4![]() ﹣6)
﹣6)
=7![]() ﹣12.
﹣12.
故答案为7![]() ﹣12.
﹣12.


科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=BC=5,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,三角板的两直角边分别交直线AB、BC于E、F两点.
(1)如图①,若O为AC的中点,点E、F分别在边AB、BC上.
①当△OFC是等腰直角三角形时,∠FOC= ;
②求证:OE=OF;
(2)如图②,若AO:AC=1:4时,OE和OF有怎样的数量关系?证明你发现的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
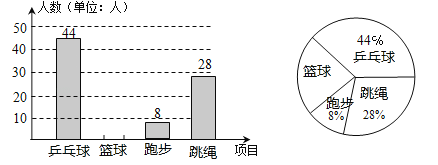
【题目】某校开展“阳光体育”活动,决定开设乒乓球、篮球、跑步、跳绳这四种运动项目,学生只能选择其中一种,为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成两张不完整的统计图,请你结合图中的信息解答下列问题:
(1)样本中喜欢篮球项目的人数百分比是 ;其所在扇形统计图中的圆心角的度数是 ;
(2)把条形统计图补画完整并注明人数;
(3)已知该校有1000名学生,根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°,AB=8cm,AD=10cm,点P在边BC上从B向C运动,点Q在边DA上从D向A运动,如果P,Q运动的速度都为每秒1cm,那么当运动时间t=_____秒时,四边形ABPQ是直角梯形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在边AB、BC上,且AE=![]() AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,下列结论:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8![]() ,其中正确的结论是______(只填序号).
,其中正确的结论是______(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
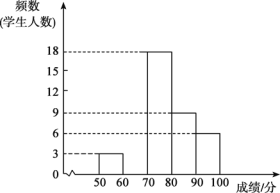
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com