练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把9m2﹣36n2分解因式的结果是

    【答案】9（m﹣2n）（（m+2n）
    【解析】解：9m2﹣36n2
    =9（m2﹣4n2）
    =9（m﹣2n）（（m+2n）．
    所以答案是：9（m﹣2n）（（m+2n）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在圆心角为90°的扇形OAB中，半径OA=4，C为的中点，D、E分别为OA，OB的中点，则图中阴影部分的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，∠BAC=90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与射线CF相交于点G．

    （1）若点D在线段BC上，如图1．

    ①依题意补全图1；

    ②判断BC与CG的数量关系与位置关系，并加以证明；

    （2）若点D在线段BC的延长线上，且G为CF中点，连接GE，AB=，则GE的长为_____，并简述求GE长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

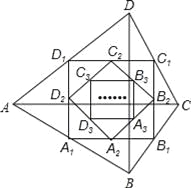
    【题目】如图，四边形ABCD中，对角线AC⊥BD，且AC=8，BD=4，各边中点分别为A1、B1、C1、D1，顺次连接得到四边形A1B1C1D1，再取各边中点A2、B2、C2、D2，顺次连接得到四边形A2B2C2D2，…，依此类推，这样得到四边形AnBnCnDn，则四边形AnBnCnDn的面积为（ ）

    A. B. C. D. 不确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是 （ ）

    A. (x＋2y)(x＋2y)＝x2＋4y2B. (x－2)2＝x2－4

    C. (x＋2)(x－3)＝x2＋x－6D. (－x－1)(x－1)＝1－x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

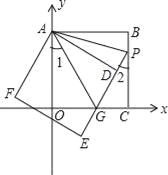
    【题目】如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（3，3）．将正方形ABCO绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．

    （1）求证：△AOG≌△ADG；

    （2）求∠PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；

    （3）当∠1=∠2时，求直线PE的解析式；

    （4）在（3）的条件下，直线PE上是否存在点M，使以M、A、G为顶点的三角形是等腰三角形？若存在，请直接写出M点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：a2﹣25=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由四舍五入法得到的近似数8.30万，它是精确到（ ）位．

    A. 精确到百分位 B. 精确到百位 C. 精确到千位 D. 精确到万位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种．如图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中BC段是双曲线的一部分．请根据图中信息解答下列问题：

    （1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？

    （2）求k的值；

    （3）当x=16时，大棚内的温度约为多少度？

    查看答案和解析>>

    同步练习册答案