
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=![]() ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.

【答案】(1)①见解析;②BC=CG,理由见解析; (2) ![]()
【解析】试题分析: (1)①依题意补全图形,如图1所示,②判断出△BAD≌△CAF即可;
(2)先判断出△BAD≌△CAF,得到BD=CF,BG⊥CF,得到直角三角形,利用勾股定理计算即可.
试题解析:
(1)证明:①依题意补全图形,如图1所示,
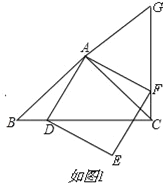
②BC⊥CG,BC=CG;
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
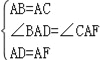
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,
∴∠ACF+∠ACB=90°,
∴BC⊥CG;
∵点G是BA延长线上的点,
BC=CG
(2)如图,
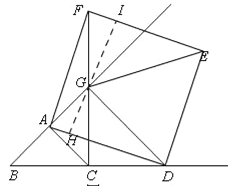
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD﹣∠DAC=90°,
∠DAF=∠CAF﹣∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
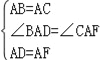
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD=45°,BD=CF,
∴∠ACF+∠ACB=90°,
∴BC⊥CF;
∵AB=![]() ,BC=CD=CG=GF=2,
,BC=CD=CG=GF=2,
∴在Rt△AGH中,根据勾股定理得,AG=![]() ,
,
∴在Rt△AGH中,根据勾股定理的,DG=2![]() ,
,
∵AD=![]() ,
,
∴AH=![]() ,HG=
,HG=![]() ,
,
∴GI=AD﹣HG=![]() ,
,
∴GE=![]() =
=![]()
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.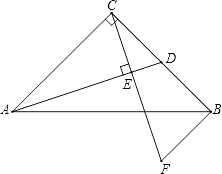
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】找规律:21-20=20 ;22-21=21 ;23-22=2 2;………利用你的发现,求20+21+22+23+…+22018+22019的值是( )
A. 22019 -1B. 22019 +1C. 22020 -1D. 22020 +1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B(2,1),AB∥y轴,且AB=4,则A的坐标是( )
A. (2,-3)B. (2,5)C. (2,-3)或(2,5)D. (6,1)或(-2,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com