
 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3. 科目:初中数学 来源: 题型:解答题
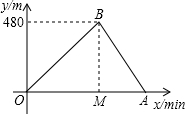 小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
小志和小明选择一个土坡进行跑步训练,他们按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚,两人上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍,设两人出发xmin后距出发点的距离为ym,图中折线表示小志在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
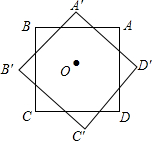 如图,已知正方形ABCD的边长为2,点O是正方形ABCD的中心,把正方形ABCD绕点O逆时针旋转45°得到正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分形成的正八边形的边长为2$\sqrt{2}$-2.
如图,已知正方形ABCD的边长为2,点O是正方形ABCD的中心,把正方形ABCD绕点O逆时针旋转45°得到正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分形成的正八边形的边长为2$\sqrt{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.
如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100,120 | B. | 120,110 | C. | 110,120 | D. | 120,120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com