
【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm? (结果精确到0.1cm,参考数据: ![]() ≈1.732)
≈1.732)
【答案】解:由题意得:AD⊥CE,过点B作BM⊥CE,BF⊥EA, ∵灯罩BC长为30cm,光线最佳时灯罩BC与水平线所成的角为30°,
∵CM⊥MB,即三角形CMB为直角三角形,
∴sin30°= ![]() =
= ![]() ,
,
∴CM=15cm,
在直角三角形ABF中,sin60°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:BF=20 ![]() ,
,
又∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20 ![]() +2≈51.6cm.
+2≈51.6cm.
答:此时灯罩顶端C到桌面的高度CE是51.6cm.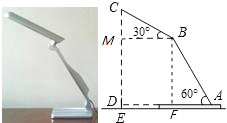
【解析】根据sin30°= ![]() ,求出CM的长,根据sin60°=
,求出CM的长,根据sin60°= ![]() ,求出BF的长,得出CE的长,即可得出CE的长.
,求出BF的长,得出CE的长,即可得出CE的长.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC. 
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y= ![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.图象经过点(1,﹣1)
B.图象位于第二、四象限
C.图象是中心对称图形
D.当x<0时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至上海的铁路里程为650km.从徐州乘“C”字头列车A,“D”字头列车B都可到达上海,已知A车的平均速度为B车的2倍,且行驶时间比B车少2.5h.
(1)设A车的平均速度是xkm/h,根据题意,可列分式方程:;
(2)求A车的平均速度及行驶时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F. 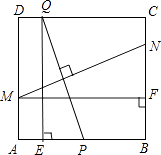
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:22+(﹣1)4+( ![]() ﹣2)0﹣|﹣3|;
﹣2)0﹣|﹣3|;
(2)先化简,再求值:(4ab3﹣8a2b2)÷4ab+(2a+b)(2a﹣b),其中a=2,b=1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com