
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
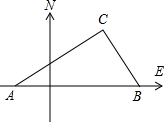 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
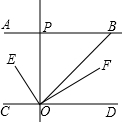 如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2\\ y=-4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=4\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-2\\ y=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-2\\ y=-4\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=$\frac{1}{3}{x^2}$+bx+c的图象与y轴交于点A,与双曲线y=$\frac{8}{x}$有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是-6.
如图,在平面直角坐标系xOy中,二次函数y=$\frac{1}{3}{x^2}$+bx+c的图象与y轴交于点A,与双曲线y=$\frac{8}{x}$有一个公共点B,它的横坐标为4,过点B作直线l∥x轴,与该二次函数图象交于另一个点C,直线AC在y轴上的截距是-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com