
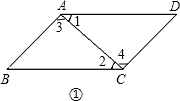
 (1)∵∠1+∠2=90°,∠1+∠3=90°(已知)
(1)∵∠1+∠2=90°,∠1+∠3=90°(已知)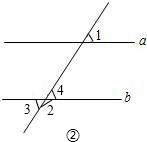 (3)如图②,直线a∥b,∠3=85°,求∠1,∠2的度数.
(3)如图②,直线a∥b,∠3=85°,求∠1,∠2的度数. 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
 19、工人师傅为了检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图1所示的工件槽,其中工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A,B,E三个接触点,该球的大小就符合要求.图2是过球心O及A,B,E三个接触点的截面示意图.已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD,BD⊥CD.请你结合图1中的数据,计算这种铁球的直径.
19、工人师傅为了检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图1所示的工件槽,其中工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A,B,E三个接触点,该球的大小就符合要求.图2是过球心O及A,B,E三个接触点的截面示意图.已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD,BD⊥CD.请你结合图1中的数据,计算这种铁球的直径.查看答案和解析>>
科目:初中数学 来源: 题型:
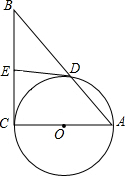 如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,交AB于D,E为BC中点,连ED.
如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,交AB于D,E为BC中点,连ED.查看答案和解析>>
科目:初中数学 来源: 题型:
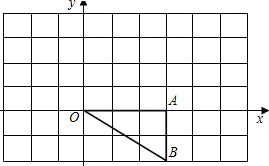 AB绕点O按逆时针方向旋转90°得到△OA′B′.
AB绕点O按逆时针方向旋转90°得到△OA′B′. | AA′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com