Question

如图1，直线y=-2x+8分别交y轴、x轴于A、B两点．
（1）求点A、B的坐标：
（2）如图1，点P为线段AB上的动点（点P不与点A、B重合），过点P作PE⊥x轴于点E，作PF⊥y轴于点F，求矩形PEOF的面积S₁与点P的横坐标m之间的函数关系式，并求出当m为何值时，S₁最大，最大值是多少？
（3）在（2）的条件下，当S₁最大时，将直线l从与直线AB重合的位置出发，沿y轴负方向向下平移a（0＜a≤8）个单位，设直线l扫过矩形PEOF的面积为S₂，求S₂与a之间的函数关系式，并在图2中画出他们之间的函数关系图象（画出草图即可）．

Answer 1

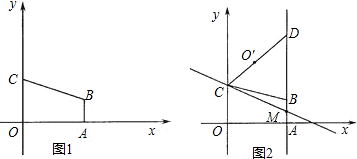
解：（1）在y=-2x+8中，令x=0，解得y=8，则A的坐标是（0，8）；
令y=0，解得x=4，则B的坐标是（4，0）；

（2）在y=-2x+8中令x=m，则y=-2m+8
则S₁=m（-2m+8），即S₁=-2m²+8m，
当m=-=2时，S₁有最大值是-2×2²+8×2=8，此时P的坐标是（2，4）；

（3）∵P的坐标是（2，4），
∴S_矩形PEOF=8，E的坐标是（2，0），F的坐标是（0，4），
设过F切平行于AB的直线解析式是：y=-2x+b，则把（0，4）代入得：b=4，则解析式是y=-2x+b，
在y=-2x+4中，令y=0，解得：x=2，则一定经过点E．
则当0＜a≤4时，直线l扫过矩形PEOF的部分是直角三角形，设向下平移a个单位长度，则直线的解析式是：y=-2x+8-a，设与PF交于点M，在y=-2x+8-a中令y=4，解得：x=2-a，则M的坐标是（2-a，4），则PM=a；
设与PE交于点N，在y=-2x+8-a中令x=2，解得：y=4-a，则N的坐标是（2，4-a），则PN=a，则S₁=PM•PN=×a•a=a²；
当4＜a≤8时，设直线与y轴交点是G，则OG=8-a，设与x轴的交点是H，则OH=（8-a）=4-a，
S_△OGH=OG•OH=（8-a）•（4-a）=（8-a）²．
则S₁=8-（8-a）²．
即S₁=-a²+4a-8．
分析：（1）在y=-2x+8中，令x=0，即可求得A的纵坐标，令y=0，即可求得B的横坐标，即可求解；
（2）利用m表示出P的横纵坐标，即可得到矩形PEOF的边长，利用函数的性质即可求得S₁的最大值；
（3）根据（2）求得P的坐标，以及E、F的坐标，利用三角形的面积公式即可求得函数的解析式．
点评：本题待定系数法求函数的解析式，二次函数的性质以及三角形的面积的综合应用，正确进行讨论是关键．