
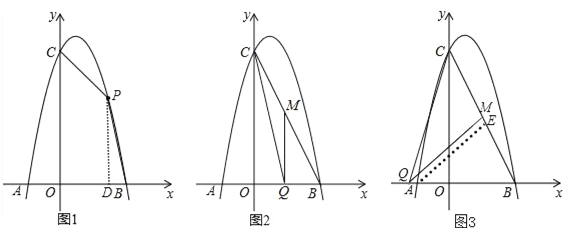
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)6;(3)Q(
;(2)6;(3)Q(![]() ,0)或Q(
,0)或Q(![]() ,0).
,0).
【解析】试题分析:(1)由对称轴的对称性得出点A的坐标,由待定系数法求出抛物线的解析式;
(2)作辅助线把四边形COBP分成梯形和直角三角形,表示出面积S,化简后是一个关于S的二次函数,求最值即可;
(3)画出符合条件的Q点,只有一种,①利用平行相似得对应高的比和对应边的比相等列比例式;②在直角△OCQ和直角△CQM利用勾股定理列方程;两方程式组成方程组求解并取舍.
试题解析:(1)由对称性得:A(﹣1,0),设抛物线的解析式为:y=a(x+1)(x﹣2),把C(0,4)代入:4=﹣2a,a=﹣2,∴y=﹣2(x+1)(x﹣2),∴抛物线的解析式为: ![]() ;
;
(2)如图1,设点P(m, ![]() ),过P作PD⊥x轴,垂足为D,∴S=S梯形+S△PDB=
),过P作PD⊥x轴,垂足为D,∴S=S梯形+S△PDB=![]() ,∴S=
,∴S=![]() =
=![]() ,∵﹣2<0,∴S有最大值,则S大=6;
,∵﹣2<0,∴S有最大值,则S大=6;
(3)存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形,理由是:
分以下两种情况:
①当∠BQM=90°时,如图2:
∵∠CMQ>90°,∴只能CM=MQ.
设直线BC的解析式为:y=kx+b,把B(2,0)、C(0,4)代入得: ![]() ,解得:
,解得: ![]() ,∴直线BC的解析式为:y=﹣2x+4,,∴直线BC的解析式为:y=﹣2x+4,设M(m,﹣2m+4),则MQ=﹣2m+4,OQ=m,BQ=2﹣m,在Rt△OBC中,BC=
,∴直线BC的解析式为:y=﹣2x+4,,∴直线BC的解析式为:y=﹣2x+4,设M(m,﹣2m+4),则MQ=﹣2m+4,OQ=m,BQ=2﹣m,在Rt△OBC中,BC=![]() =
=![]() =
=![]() ,∵MQ∥OC,∴△BMQ∽BCO,∴
,∵MQ∥OC,∴△BMQ∽BCO,∴![]() ,即
,即![]() ,∴BM=
,∴BM=![]() =
= ![]() ,∴CM=BC﹣BM=
,∴CM=BC﹣BM=![]() =
= ![]() ,∵CM=MQ,∴﹣2m+4=
,∵CM=MQ,∴﹣2m+4= ![]() ,m=
,m=![]() =
=![]() ,∴Q(
,∴Q(![]() ,0).
,0).
②当∠QMB=90°时,如图3:
设M(a,﹣2a+4),过A作AE⊥BC,垂足为E,则AE的解析式为: ![]() ,则直线BC与直线AE的交点E(1.4,1.2),设Q(﹣x,0)(x>0),∵AE∥QM,∴△ABE∽△QBM,∴
,则直线BC与直线AE的交点E(1.4,1.2),设Q(﹣x,0)(x>0),∵AE∥QM,∴△ABE∽△QBM,∴![]() ①,由勾股定理得:
①,由勾股定理得: ![]() ②,由①②得:
②,由①②得: ![]() =4(舍),
=4(舍),![]() =
=![]() ,当a=
,当a=![]() 时,x=
时,x=![]() ,∴Q(
,∴Q(![]() ,0).
,0).
综上所述,Q点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC,其中正确的结论是(把你认为正确的结论的序号都填上). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元
(1) 求甲、乙两种商品每件的进价分别是多少元?
(2) 商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直线l外一点,在l上去两点A、B,连接AD,分别以点B、D为圆心,AD、AB的长尾半径画弧,两弧交于点C,连接CD、BC,则四边形ABCD是平行四边形,理由是 . 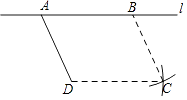
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线l1 , l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE、CF. 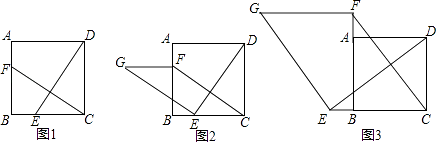
(1)求证:DE=CF;
(2)在(1)条件下,如图2,过点E作BG⊥DE,且EG=DE,连接FG,试判断:FG与CE的数量关系和位置关系?给出证明.
(3)如图3,若点E、F分别是CB、BA的延长线上的点,其他条件不变,(2)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:则这20户家庭该月用电量的众数和中位数分别是( )
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
A.7,6B.7,3C.180,160D.180,170
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com