【题目】如图1，在正方形ABCD中，点E、F分别是边BC、AB上的点，且CE=BF，连接DE、CF．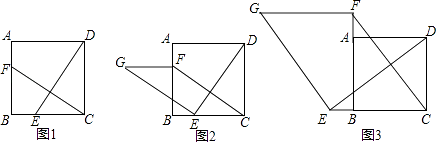
（1）求证：DE=CF；
（2）在（1）条件下，如图2，过点E作BG⊥DE，且EG=DE，连接FG，试判断：FG与CE的数量关系和位置关系？给出证明．
（3）如图3，若点E、F分别是CB、BA的延长线上的点，其他条件不变，（2）中结论是否仍然成立？请直接写出你的判断．

参考答案：

【答案】
（1）证明：∵四边形ABCD是正方形，

∴BC=CD，∠ABC=∠DCE=90°，

在△CBF和△DCE中， ，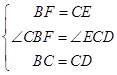

∴△CBF≌△DCE（SAS），

∴CF=DE；


（2）解：结论：GF=EC，GF∥EC，

理由：由（1）知，∠BCF=∠CDE，

∵∠BCF+∠DCF=90°，

∴∠CDE+∠DCF=90°，

∴CF⊥DE，

∵GE⊥DE，

∴EG∥CF，

∵EG=DE，CF=DE，

∴EG=CF，

∴四边形EGFC是平行四边形，

∴GF=EC，GF∥EC；


（3）解：结论仍然成立，GF=EC，GF∥EC，

理由：由（1）知，∠BCF=∠CDE，

∵∠BCF+∠DCF=90°，

∴∠CDE+∠DCF=90°，

∴CF⊥DE，

∵GE⊥DE，

∴EG∥CF，

∵EG=DE，CF=DE，

∴EG=CF，

∴四边形EGFC是平行四边形，

∴GF=EC，GF∥EC．


【解析】（1）由正方形的性质得出BC=CD，∠ABC=∠DCE=90°，进而判断出△CBF≌△DCE（SAS），即可得出结论；（2）先判断出CF⊥DE，进而判断出EG∥CF，即可判断出四边形EGFC是平行四边形，即可得出结论；（3）同（1）的方法即可得出结论．
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点，需要掌握若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积才能正确解答此题．

关闭