
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
【答案】
(1)解:设每吨水的政府补贴优惠价为m元,市场调节价为n元.
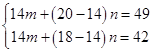 ,
,
解得: ![]() ,
,
答:每吨水的政府补贴优惠价2元,市场调节价为3.5元.
(2)解:当0≤x≤14时,y=2x;
当x>14时,y=14×2+(x﹣14)×3.5=3.5x﹣21,
故所求函数关系式为:y= 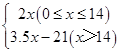 ;
;
(3)解:∵26>14,
∴小明家5月份水费为3.5×26﹣21=70元,
答:小明家5月份水费70元.
【解析】(1)设每吨水的政府补贴优惠价为m元,市场调节价为n元,根据题意列出方程组,求解此方程组即可;(2)根据用水量分别求出在两个不同的范围内y与x之间的函数关系,注意自变量的取值范围;(3)根据小明家5月份用水26吨,判断其在哪个范围内,代入相应的函数关系式求值即可.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 
(1)求点B的坐标;
(2)若△ABC的面积为4,请求出点C的坐标,并直接写出直线L2所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
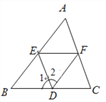
【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线l1 , l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 
(1)求证:四边形DCFE是平行四边形;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE、CF. 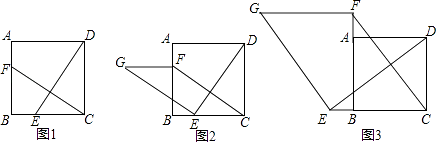
(1)求证:DE=CF;
(2)在(1)条件下,如图2,过点E作BG⊥DE,且EG=DE,连接FG,试判断:FG与CE的数量关系和位置关系?给出证明.
(3)如图3,若点E、F分别是CB、BA的延长线上的点,其他条件不变,(2)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:

①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把ax2﹣4ay2分解因式正确的是( )
A.a(x+2y)(x﹣2y)
B.a(x﹣2y)2
C.a(x﹣4y)2
D.a(x+4y)(x﹣4y)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com