
【题目】某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.

科目:初中数学 来源: 题型:
【题目】小明同学在“百度”搜索引擎中输入“中国梦,我的梦”,搜索到与之相关的结果条数为608000,这个数用科学记数法表示为( )
A. 60.8×104B. 6.08×105C. 0.608×106D. 6.08×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线l1 , l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB= ![]() .
. 
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE、CF. 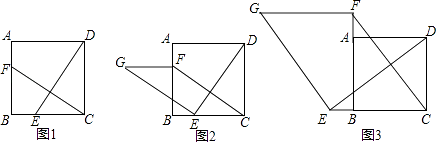
(1)求证:DE=CF;
(2)在(1)条件下,如图2,过点E作BG⊥DE,且EG=DE,连接FG,试判断:FG与CE的数量关系和位置关系?给出证明.
(3)如图3,若点E、F分别是CB、BA的延长线上的点,其他条件不变,(2)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:则这20户家庭该月用电量的众数和中位数分别是( )
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
A.7,6B.7,3C.180,160D.180,170
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:

①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
(1)如图1,当EF与斜边BC不相交时,试说明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF,BE,CF之间的数量关系,并说明理由;
(3)如图3,猜想EF,BE,CF之间又存在怎样的数量关系,写出猜想,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数)
(参考数据:sin42°≈0.67,tan42°≈0.9,sin65°≈0.91,tan65°≈2.1)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com