
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
(1)如图1,当EF与斜边BC不相交时,试说明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF,BE,CF之间的数量关系,并说明理由;
(3)如图3,猜想EF,BE,CF之间又存在怎样的数量关系,写出猜想,说明理由.

【答案】(1)理由见解析;(2)EF=BE-CF.理由见解析.
【解析】试题分析:(1)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,从而得出答案;(2)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AF-AE得出答案;(3)、根据题意得出△ABE和△CAF全等,从而得出AE=CF,BE=AF,根据EF=AE-AF得出答案.
试题解析:(1)因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠EBA+∠EAB=90°.所以∠CAF=∠EBA.
在△ABE和△CAF中,∠BEA=∠AFC,∠EBA=∠FAC,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.所以EF=EA+AF=BE+CF.
(2)EF=BE-CF.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFE=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.所以∠CAF=∠ABE.
在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,所以△BEA≌△AFC(AAS).
所以EA=FC,BE=AF.因为EF=AF-AE,所以EF=BE-CF.
(3)EF=CF-BE.理由是:因为BE⊥EA,CF⊥AF,所以∠BAC=∠BEA=∠CFA=90°.
所以∠EAB+∠CAF=90°,∠ABE+∠EAB=90°.
所以∠CAF=∠ABE.在△ABE和△ACF中,∠EBA=∠FAC,∠BEA=∠CFA,AB=AC,
所以△BEA≌△AFC(AAS).
所以EA=FC,BE=CF.因为EF=EA-AF,所以EF=CF-BE.


科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
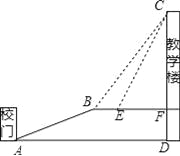
【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i;(2)求DC的长.(参考数据:tan53°≈![]() ,tan63.4°≈2)
,tan63.4°≈2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com