
 如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).
如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).分析 (1)由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),把点B坐标代入求出a即可.
(2)①)①如图1中,设点M的坐标为(m,(m+2)2),其中-2<m<0,则N点坐标(m,0).若要四边形BMAC的面积最大,只要BMA的面积最大即可,构建二次函数,利用二次函数的性质即可解决问题.
(3)有三种情形,先画出图形,利用中点坐标公式一一求解即可.
解答 解:(1)由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),
∵抛物线与y轴交于点B(0,4)
∴4=a(0+2)2
解得:a=1
∴抛物线对应的解析式为:y=(x+2)2.
(2)①如图1中,设点M的坐标为(m,(m+2)2),其中-2<m<0,
则N点坐标(m,0).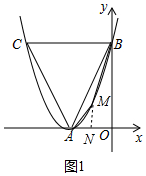
∵A、B、C是定点,
∴若要四边形BMAC的面积最大,
只要BMA的面积最大即可.
过M做MN⊥x轴于点N,则
S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2×4=4
S△AMN=$\frac{1}{2}$AN•MN=$\frac{1}{2}$×[m-(-2)]×(m+2)2=$\frac{1}{2}$(m+2)3
S梯形ONMB=$\frac{1}{2}$ON(MN+OB)
=$\frac{1}{2}$×(-m)×[(m+2)2+4]
=-$\frac{1}{2}$(m3+4m2+8m)
∴S△AMB=S△AOB-S△AMN-S梯形ONMB
=4-$\frac{1}{2}$(m+2)3-[-$\frac{1}{2}$(m3+4m2+8m)]
=-m2-2m,
当m=-1时,S△AMB最大,
∵(-1+2)2=1
∴此时点M的坐标为(-1,1).
②存在.如图2中,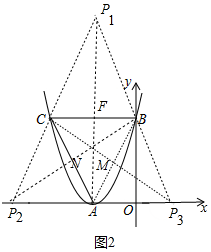
∵四边形ABP1C是平行四边形,
∴FC=FB,AF=FP1,
∵B(0,4),C(-4,4),
∴F(-2,4),
设P1(x,y),则有$\frac{-2+x}{2}$=-2,$\frac{0+y}{2}$=4,
∴x=-2,y=8,
∴P1(-2,8),同法可得P2(-6,0),P3(2,0).
所有满足条件的点P的坐标是(2,0)、(-6,0)、(-2,8).
点评 本题考查二次函数综合题、平行四边形的判定和性质、中点坐标公式、待定系数法等知识,解题的关键是灵活应用顶点式确定函数解析式,学会根据二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考常考题型.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x+y=35\\ 18x+24y=750\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=35\\ 24x+18y=750\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y=35\\ 24x-18y=750\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=35\\ 18x-24y=750\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
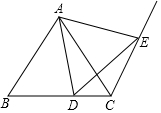 如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE
如图,△ABC是等边三角形,点D是BC上的点,点E是射线CN上的点,且CN∥AB,联结AD、AE、DE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠B=135°,则$\widehat{AC}$的长( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠B=135°,则$\widehat{AC}$的长( )| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3}{2}π$ | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com