
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)图中是否存在与△ODM相似的三角形,若存在,请找出并给于证明。
(2)设DM = x,OA=R,求R关于x 的函数关系式;是否存在整数R,使得正方形ABCD内部的扇形OAM围成的圆锥地面周长为 p ,若存在请求出此时DM的长;不存在,请说明理由。
p ,若存在请求出此时DM的长;不存在,请说明理由。
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

解(1)∵MN切⊙O于点M,∴ ………………… 1分
………………… 1分
∵

∴ …………………………… 1分
…………………………… 1分
又∵ ∴△
∴△ ∽△
∽△ , ……1分
, ……1分
(2)在Rt△ 中,
中, ,设
,设 ;
;
∴ , ………………………1分
, ………………………1分
由勾股定理得: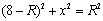 ,……………… 1分
,……………… 1分
∴ ,∴
,∴ ; ……………… 1分
; ……………… 1分
∵4<OA<8即4<R<8
∴当R=5时,∠MOA超过1800,不符合,舍去……………… 1分
当R=6时,∠MOA=1600,∴
∵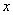 >0,,∴
>0,,∴ ……………… 1分
……………… 1分
同理当R=7时,x= ……………… 1分
……………… 1分
(3)∵ ,又
,又
且有△ ∽△
∽△ , ∴
, ∴ , ∴代入得到
, ∴代入得到 ; …………… 1分
; …………… 1分
同理 ,∴代入得到
,∴代入得到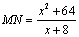 ; ……………………………………2分
; ……………………………………2分
∴△CMN的周长为P=
 .………………1分
.………………1分
在点O的运动过程中,△CMN的周长P始终为16,是一个定值.



科目:初中数学 来源: 题型:
已知:如图,在RT△ABC中,∠ACB=90°,CA=CB, O是AB的中点,点D在BA的延长线上,以D为直角顶点作RT△DEF, FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断段OM、ON的数量关系与位置关系,并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
把多项式x4一8x2+16分解因式,所得结果是( )
A.(x-2)2 (x+2)2 B. (x-4)2 (x+4)2 C.(x一4)2 D.(x-4)4
查看答案和解析>>
科目:初中数学 来源: 题型:
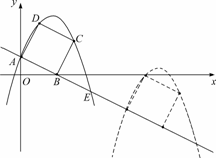
如图,已知直线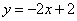 交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
(1)求抛物线的解析式;
(2)若矩形以每秒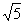 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设矩形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设矩形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
(3)在(2)的条件下,抛物线与矩形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com