
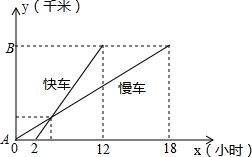
 一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题:分析 (1)观察函数图象的横坐标,可得答案;
(2)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间,可得速度;
(3)根据图象的交点,可得快车追上慢车的时间,根据函数图象的横坐标,可得慢车比快车多用的时间.
解答 解:(1)由横坐标看出慢车比快车早出发2小时,快车比慢车少用6小时到达B地;
(2)慢车18小时行驶1200千米,慢车的速度是1200÷18=$\frac{200}{3}$千米/小时;
快车10小时行驶1200千米,快车的速度是1200÷10=120千米/小时;
(3)由横坐标看出,慢车比快车多用18-10=8小时;
设慢车行驶x小时快车追上慢车,由题意,得
$\frac{200}{3}$x=120(x-2),
解得x=$\frac{9}{2}$.
故慢车出发$\frac{9}{2}$小时,快车追上慢车.
点评 本题考查了函数图象,观察函数图象的横坐标得出时间,函数图象的纵坐标得出路程.


科目:初中数学 来源: 题型:解答题
 滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:
滨湖区举行“我的中国梦”演讲比赛,某校中学组根据初赛成绩在七八年级分别选出10名同学参加比赛,这些选手的决赛成绩如图所示:| 成绩统计 | 众数 | 平均数 | 方差 |
| 七年级 | 80 | 85.7 | 39.61 |
| 八年级 | 85 | 85.7 | 27.81 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.
某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com