
 如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:
如图,将长方形ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处.已知CE=3cm,AB=8cm. 求:| AB |
| CF |
| AF |
| EF |
| 1 |
| 2 |
 解:(1)如图,∵CD=AB=8,CE=3,
解:(1)如图,∵CD=AB=8,CE=3,| AB |
| CF |
| AF |
| EF |
| 1 |
| 2 |


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
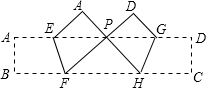 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
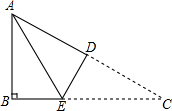 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.
某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com