
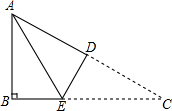
 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
科目:初中数学 来源: 题型:
| A、平均数 | B、中位数 |
| C、众数 | D、方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处,…请你根据①②步骤解答下列问题:
八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处,…请你根据①②步骤解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,现将△ABC进行翻折,点C恰落在边AB上的点D处,折痕为EF,此时恰有∠DEF=∠A,则AD与BD的大小关系是
如图,在Rt△ABC中,∠C=90°,现将△ABC进行翻折,点C恰落在边AB上的点D处,折痕为EF,此时恰有∠DEF=∠A,则AD与BD的大小关系是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,∠C=90°,D是边AB上的一点,MD⊥AB,垂足为D,且DM=AC,在边AB上取点E,连接ME,使ME=AB,若BC=
如图,在△ABC中,∠C=90°,D是边AB上的一点,MD⊥AB,垂足为D,且DM=AC,在边AB上取点E,连接ME,使ME=AB,若BC=| 6 |
| A、3 | ||
| B、4 | ||
C、
| ||
| D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(110-x)吨 |
| B、(100-x)吨 |
| C、(x-20)吨 |
| D、(x-10)吨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com