
 已知抛物线y=-
已知抛物线y=-| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 6 |
| 6 |
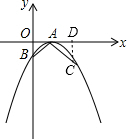 作CD⊥x轴于D,如图,
作CD⊥x轴于D,如图,| OA |
| CD |
| OB |
| AD |
| 2 |
| CD |
| 1 |
| AD |
| 1 |
| 4 |
| 1 |
| 4 |
| 6 |
| 6 |
| 6 |
| 6 |


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
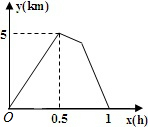 甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了
甲、乙二人同时从A地到B地,甲骑自行车,乙步行,甲到B地后休息了十分钟然后以相同的速度返回,在返回途中与乙相遇,甲、乙二人之间的距离y(km)与乙步行时间x(h)之间的关系如图,则甲从出发到返回与乙相遇共走了查看答案和解析>>
科目:初中数学 来源: 题型:
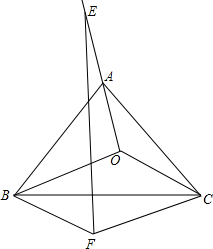 已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系.
已知O是等边三角形ABC所在平面上任意一点,连接OA并延长到E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC连接EF,请探索FE与BC之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:
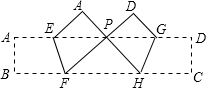 把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?
把长方形纸条ABCD沿EF,GH同时折叠,B、C两点恰好都落在AD边的P点处,若∠FPH=90°,PF=8,PH=6,则长方形ABCD的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
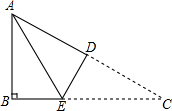 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )
如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com