
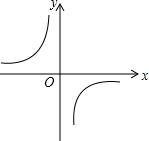
 反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )
反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )| A. | 常数m<1 | |
| B. | y随x的增大而增大 | |
| C. | 若A(-1,h),B(2,k)在图象上,则h<k | |
| D. | 若P(-x,y)在图象上,则P′(x,-y)也在图象上 |
分析 A:根据双曲线的两支分别位于第二、第四象限,可得m<0,据此解答即可.
B:在每一象限内y随x的增大而增大,据此判断即可.
C:根据y=$\frac{m}{x}$,分别求出h、k的值是多少,再比较它们的大小关系即可.
D:根据反比例函数y=$\frac{m}{x}$的图象成中心对称,可得若P(-x,y)在图象上,则P′(x,-y)也在图象上,据此解答即可.
解答 解:∵双曲线的两支分别位于第二、第四象限,
∴m<0,
∴选项A不正确;
∵在每一象限内y随x的增大而增大,
∴选项B不正确;
∵h=$\frac{m}{-1}$=-m>0,k=$\frac{m}{2}<0$,
∴h>k,
∴选项C不正确;
∵反比例函数y=$\frac{m}{x}$的图象成中心对称,
∴若P(-x,y)在图象上,则P′(x,-y)也在图象上,
∴选项D正确.
故选:D.
点评 此题主要考查了反比例函数的性质,要熟练掌握,解答此题的关键是要明确:(1)反比例函数y=xk(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )
如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )| A. | $\frac{1}{3}$cm | B. | $\frac{2}{3}$cm | C. | 1cm | D. | $\frac{4}{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
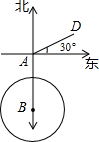 如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风正以40海里/时的速度由南向北移动,距台风20$\sqrt{2}$海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.
如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风正以40海里/时的速度由南向北移动,距台风20$\sqrt{2}$海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
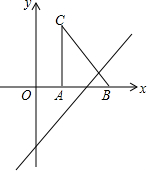 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )| A. | 80 | B. | 88 | C. | 96 | D. | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com